题目内容
我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等.那么在什么情况下,它们会全等?
阅读与证明:
(1)这两个三角形均为直角三角形,显然它们全等.
(2)这两个三角形均为钝角三角形,可证它们全等.
(3)这两个三角形均为锐角三角形,也可证全等.
请你在上述的说法的2或者3中选择一个进行证明(提示:请写出已知与求证)
阅读与证明:
(1)这两个三角形均为直角三角形,显然它们全等.
(2)这两个三角形均为钝角三角形,可证它们全等.
(3)这两个三角形均为锐角三角形,也可证全等.
请你在上述的说法的2或者3中选择一个进行证明(提示:请写出已知与求证)
考点:全等三角形的判定
专题:探究型
分析:过B作BD⊥AC于D,过B1作B1D1⊥B1C1于D1,得出∠BDA=∠B1D1A1=∠BDC=∠B1D1C1=90°,根据SAS证△BDC≌△B1D1C1,推出BD=B1D1,根据HL证Rt△BDA≌Rt△B1D1A1,推出∠A=∠A1,根据AAS推出△ABC≌△A1B1C1即可.
解答:已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1.
求证:△ABC≌△A1B1C1.
 证明:过B作BD⊥AC于D,过B1作B1D1⊥B1C1于D1,
证明:过B作BD⊥AC于D,过B1作B1D1⊥B1C1于D1,
则∠BDA=∠B1D1A1=∠BDC=∠B1D1C1=90°,
在△BDC和△B1D1C1中,
,
∴△BDC≌△B1D1C1,
∴BD=B1D1,
在Rt△BDA和Rt△B1D1A1中
∴Rt△BDA≌Rt△B1D1A1(HL),
∴∠A=∠A1,
在△ABC和△A1B1C1中
∴△ABC≌△A1B1C1(AAS).
求证:△ABC≌△A1B1C1.
 证明:过B作BD⊥AC于D,过B1作B1D1⊥B1C1于D1,
证明:过B作BD⊥AC于D,过B1作B1D1⊥B1C1于D1,则∠BDA=∠B1D1A1=∠BDC=∠B1D1C1=90°,
在△BDC和△B1D1C1中,
|
∴△BDC≌△B1D1C1,
∴BD=B1D1,
在Rt△BDA和Rt△B1D1A1中
|
∴Rt△BDA≌Rt△B1D1A1(HL),
∴∠A=∠A1,
在△ABC和△A1B1C1中
|
∴△ABC≌△A1B1C1(AAS).
点评:本题考查了全等三角形的性质和判定的应用,主要考查学生的推理能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

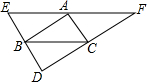 如图,已知EF、ED、FD分别过△ABC的顶点A、B、C,且EF∥BC,ED∥AC,FD∥AB,求证:点A、B、C分别是线段EF、ED、DF的中点.
如图,已知EF、ED、FD分别过△ABC的顶点A、B、C,且EF∥BC,ED∥AC,FD∥AB,求证:点A、B、C分别是线段EF、ED、DF的中点.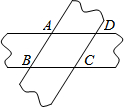 用两张平行的纸条交叉重叠放在一起,则四边形ABCD为
用两张平行的纸条交叉重叠放在一起,则四边形ABCD为