题目内容
 如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为6和8,那么点P到矩形的两条对角线AC和BD的距离之和是
如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为6和8,那么点P到矩形的两条对角线AC和BD的距离之和是考点:矩形的性质
专题:几何图形问题
分析:首先连接OP,由矩形的两条边AB、BC的长分别为6和8,可求得OA=OD=5,△AOD的面积,然后由S△AOD=S△AOP+S△DOP=
OA•PE+
OD•PF求得答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答: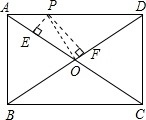 解:连接OP,
解:连接OP,
∵矩形的两条边AB、BC的长分别为6和8,
∴S矩形ABCD=AB•BC=48,OA=OC,OB=OD,AC=BD=
=10,
∴OA=OD=5,
∴S△ACD=
S矩形ABCD=24,
∴S△AOD=
S△ACD=12,
∵S△AOD=S△AOP+S△DOP=
OA•PE+
OD•PF=
×5×PE+
×5×PF=
(PE+PF)=12,
解得:PE+PF=4.8.
故答案为:4.8.
 解:连接OP,
解:连接OP,∵矩形的两条边AB、BC的长分别为6和8,
∴S矩形ABCD=AB•BC=48,OA=OC,OB=OD,AC=BD=
| AB2+BC2 |
∴OA=OD=5,
∴S△ACD=
| 1 |
| 2 |
∴S△AOD=
| 1 |
| 2 |
∵S△AOD=S△AOP+S△DOP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
解得:PE+PF=4.8.
故答案为:4.8.
点评:此题考查了矩形的性质以及三角形面积问题.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
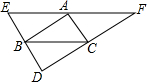 如图,已知EF、ED、FD分别过△ABC的顶点A、B、C,且EF∥BC,ED∥AC,FD∥AB,求证:点A、B、C分别是线段EF、ED、DF的中点.
如图,已知EF、ED、FD分别过△ABC的顶点A、B、C,且EF∥BC,ED∥AC,FD∥AB,求证:点A、B、C分别是线段EF、ED、DF的中点.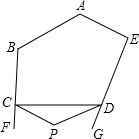 如图,五边形ABCDE中,∠BCD、∠EDC的外角分别是∠FCD、∠GDC,CP、DP分别平分∠FCD和∠GDC且相交于点P,若∠A=140°,∠B=120°,∠E=90°,∠P=
如图,五边形ABCDE中,∠BCD、∠EDC的外角分别是∠FCD、∠GDC,CP、DP分别平分∠FCD和∠GDC且相交于点P,若∠A=140°,∠B=120°,∠E=90°,∠P=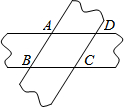 用两张平行的纸条交叉重叠放在一起,则四边形ABCD为
用两张平行的纸条交叉重叠放在一起,则四边形ABCD为 如图,在四边形ABCD中,AD∥BC,AD=15cm,BC=10cm,P、Q分别从A、C同时出发,P以3cm/s的速度由A向D运动,Q以2cm/s的速度由C出发向B运动,运动
如图,在四边形ABCD中,AD∥BC,AD=15cm,BC=10cm,P、Q分别从A、C同时出发,P以3cm/s的速度由A向D运动,Q以2cm/s的速度由C出发向B运动,运动