题目内容
若a、b为实数,且a2+b2+2a+8b+17=0,则
+
= .
|
|
考点:因式分解-运用公式法,非负数的性质:偶次方
专题:计算题,因式分解
分析:首先根据a2+b2+2a+8b+17=0可得(a+1)2+(b+4)2=0,再根据偶次幂具有非负性可得a+1=0,b+4=0,算出a、b的值,再代入计算出
+
的值.
|
|
解答:解:∵a2+b2+2a+8b+17=0,
∴(a+1)2+(b+4)2=0,
∴a+1=0,b+4=0,
解得a=-1,b=-4,
+
=
+2=2
,
故答案为:2
.
∴(a+1)2+(b+4)2=0,
∴a+1=0,b+4=0,
解得a=-1,b=-4,
|
|
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:2
| 1 |
| 2 |
点评:此题主要考查了公式法分解因式和偶次幂的性质,关键是掌握偶次幂具有非负性.

练习册系列答案
相关题目
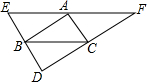 如图,已知EF、ED、FD分别过△ABC的顶点A、B、C,且EF∥BC,ED∥AC,FD∥AB,求证:点A、B、C分别是线段EF、ED、DF的中点.
如图,已知EF、ED、FD分别过△ABC的顶点A、B、C,且EF∥BC,ED∥AC,FD∥AB,求证:点A、B、C分别是线段EF、ED、DF的中点.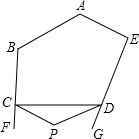 如图,五边形ABCDE中,∠BCD、∠EDC的外角分别是∠FCD、∠GDC,CP、DP分别平分∠FCD和∠GDC且相交于点P,若∠A=140°,∠B=120°,∠E=90°,∠P=
如图,五边形ABCDE中,∠BCD、∠EDC的外角分别是∠FCD、∠GDC,CP、DP分别平分∠FCD和∠GDC且相交于点P,若∠A=140°,∠B=120°,∠E=90°,∠P=