题目内容
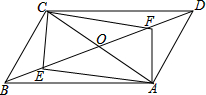 如图,在平行四边形ABCD中,AC,BD相交于点O,AC=6,BD=8,∠AOD=65°,点E在BO上,AF∥CE交BD于点F.
如图,在平行四边形ABCD中,AC,BD相交于点O,AC=6,BD=8,∠AOD=65°,点E在BO上,AF∥CE交BD于点F.(1)求证:四边形AFCE是平行四边形.
(2)当点E在边BO上移动时,平行四边形AFCE能否为矩形?若能,此时BE的长为等于多少(直接写出结果)?若不能,请说明理由.
(3)当点E在边BO上移动时,平行四边形AFCE能否为菱形?若能,此BE的长为等于多少(直接写出结果)?若不能,请说明理由.
考点:平行四边形的判定与性质,菱形的判定,矩形的判定
专题:几何动点问题,几何综合题,数形结合
分析:(1)由在平行四边形ABCD中,AF∥CE,易证得△AOF≌△COE,则可得OE=OF,又由OA=OC,即可判定四边形AFCE是平行四边形.
(2)当EF=AC时,平行四边形AFCE为矩形,由AC=6,BD=8,即可求得此时BE的长;
(3)由∠AOD=65°,可得AC与BD不垂直,即可得平行四边形AFCE不能为菱形.
(2)当EF=AC时,平行四边形AFCE为矩形,由AC=6,BD=8,即可求得此时BE的长;
(3)由∠AOD=65°,可得AC与BD不垂直,即可得平行四边形AFCE不能为菱形.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AF∥CE,
∴∠OAF=∠OCE,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴OE=OF,
∴四边形AFCE是平行四边形;
(2)平行四边形AFCE能为矩形.
理由:∵四边形AFCE是平行四边形,
∴当EF=AC=6时,平行四边形AFCE为矩形,
∵OE=OF,OB=OD,
∴BE=CF,
∴2BE+EF=BD,
即2BE+6=8,
解得:BE=1,
∴当BE=1时,平行四边形AFCE为矩形;
(3)平行四边形AFCE不能为菱形.
理由:∵四边形AFCE是平行四边形,且∠AOD=65°,
即AC与BD不垂直,
∴平行四边形AFCE不能为菱形.
∴OA=OC,OB=OD,
∵AF∥CE,
∴∠OAF=∠OCE,
在△AOF和△COE中,
|
∴△AOF≌△COE(ASA),
∴OE=OF,
∴四边形AFCE是平行四边形;
(2)平行四边形AFCE能为矩形.
理由:∵四边形AFCE是平行四边形,
∴当EF=AC=6时,平行四边形AFCE为矩形,
∵OE=OF,OB=OD,
∴BE=CF,
∴2BE+EF=BD,
即2BE+6=8,
解得:BE=1,
∴当BE=1时,平行四边形AFCE为矩形;
(3)平行四边形AFCE不能为菱形.
理由:∵四边形AFCE是平行四边形,且∠AOD=65°,
即AC与BD不垂直,
∴平行四边形AFCE不能为菱形.
点评:此题考查了平行四边形的判定与性质、矩形的判定、菱形的判定以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目

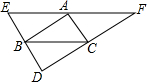 如图,已知EF、ED、FD分别过△ABC的顶点A、B、C,且EF∥BC,ED∥AC,FD∥AB,求证:点A、B、C分别是线段EF、ED、DF的中点.
如图,已知EF、ED、FD分别过△ABC的顶点A、B、C,且EF∥BC,ED∥AC,FD∥AB,求证:点A、B、C分别是线段EF、ED、DF的中点.