题目内容
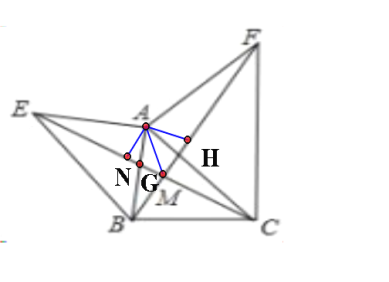
【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.
(1)问线段EC与BF数量关系和位置关系?并给予证明.
(2)连AM,请问∠AME的大小是多少,如能求写出过程;不能求,写出理由.

【答案】(1)EC⊥BF, EC=BF(2)∠AME=45°.
【解析】
(1)先由条件可以得出∠EAC=∠FAB,再证明△EAC≌△BAF就可以得出结论.
(2)作AN⊥EC,AH⊥BF,通过(1)中已知条件证明Rt△AMH ≌Rt△AMN,即可求解.
(1)理由: 设AB与EC的交点为G
∵AE⊥AB,AF⊥AC,
∴∠EAB=∠CAF=90°,
∴∠EAB+∠BAC=∠CAF+∠BAC,
∴∠EAC=∠FAB
在△EAC和△BAF中,AE=AB, ∠EAC=∠FAB,AF=AC
∴△EAC≌△BAF
∴EC=BF, ∠AEC=∠FBA
∵∠AEG+∠AGE=90°,∠AGE=∠BGM,
∴∠ABF+∠BGM=90°
∴∠BME=90°,
∴EC⊥BF.
(2)作AN⊥EC,AH⊥BF
∵△EAC≌△BAF,AN⊥EC,AH⊥BF
∴AH=AN
∵AM⊥EC,AN⊥BF
∴Rt△AMH 和Rt△AMN中,AH=AN,AM=AM
∴Rt△AMH ≌Rt△AMN(HL)
∴∠AMH =∠AMN
∵EC⊥BF
∴∠AME=45°.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目