题目内容
【题目】如图,CD是⊙O的直径,已知∠1=30°,则∠2=( ) 
A.30°
B.45°
C.60°
D.70°
【答案】C
【解析】解:如图,连接AD. 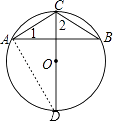
∵CD是⊙O的直径,
∴∠CAD=90°(直径所对的圆周角是90°);
在Rt△ABC中,∠CAD=90°,∠1=30°,
∴∠DAB=60°;
又∵∠DAB=∠2(同弧所对的圆周角相等),
∴∠2=60°,
故选C.
连接AD,构建直角三角形ACD.根据直径所对的圆周角是90°知三角形ACD是直角三角形,然后在Rt△ABC中求得∠BAD=60°;然后由圆周角定理(同弧所对的圆周角相等)求∠2的度数即可.本题考查了圆周角定理.解答此题的关键是借助辅助线AD,将隐含是题干中的已知条件△ACD是直角三角形展现出来,然后根据直角三角形的两个锐角互余求得∠DAB=60°.

练习册系列答案
相关题目