题目内容
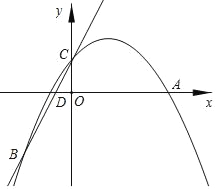
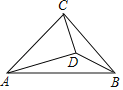
【题目】如图,在Rt△ABC中,AC=BC,点D是△ABC内一点,若AC=AD,∠CAD=30°,连接BD,则∠ADB的度数为( )
A.120°B.135°C.150°D.165°
【答案】B
【解析】
先根据△ABC是等腰直角三角形得:∠CAB=∠ABC=45°,作辅助线,构建全等三角形,证明△CDB≌△AED,则∠ADE=∠CBD,ED=BD,设∠CBD=x,则∠ADE=x,∠DEB=∠DBE=15+x,根据∠ABC=45°列方程可求x的值,根据三角形内角和得∠BDC=150°,最后由周角得出结论.
∵AC=BC,∠ACB=90°,
∴∠CAB=∠ABC=45°,
∵AC=AD,
∴AD=BC,
∵∠CAD=30°,
∴∠ACD=∠ADC=75°,
∠DAB=45°﹣30°=15°,
∴∠DCB=90°﹣75°=15°,
∴∠EAD=∠DCB,
在AB上取一点E,使AE=CD,连接DE,
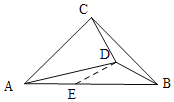
在△CDB和△AED中,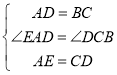 ,
,
∴△CDB≌△AED(SAS),
∴∠ADE=∠CBD,ED=BD,
∴∠DEB=∠DBE,
设∠CBD=x,则∠ADE=x,∠DEB=∠DBE=15+x,
∵∠ABC=45°,
∴x+15+x=45,
∴x=15°,
∴∠DCB=∠DBC=15°,
∴∠BDC=180°﹣15°﹣15°=150°,
∴∠ADB=360°﹣75°﹣150°=135°;
故选:B.

练习册系列答案
相关题目