��Ŀ����
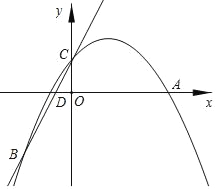
����Ŀ����֪������y=ax2+bx+2����A��5��0���͵�B����3����4������y�ύ�ڵ�C��
��1����������y=ax2+bx+2�ĺ�������ʽ��
��2����ֱ��BC�ĺ�������ʽ��
��3����E�ǵ�B����y��ĶԳƵ㣬����AE��BE����P������EB��BC�ϵ�һ�����㣬
������P���߶�BC��ʱ������EP����EP��BC����ֱ��д���߶�BP���߶�AE�Ĺ�ϵ��
������P��x��Ĵ��������C����y��Ĵ��߽��ڵ�M������M�����C�غ�ʱ����M����ֱ��PC�ĶԳƵ�Ϊ��M�䣬�����M��ǡ�����������ϣ���ֱ��д����ʱ��P�����꣮
���𰸡���1��y=��![]() x2+
x2+![]() x+2����2��y=2x+2����3�����߶�BP���߶�AE�Ĺ�ϵ�����ֱ������P������Ϊ������4+2
x+2����2��y=2x+2����3�����߶�BP���߶�AE�Ĺ�ϵ�����ֱ������P������Ϊ������4+2![]() ����8+4
����8+4![]() ����4��2
����4��2![]() ����8��4
����8��4![]() ����0����4����
����0����4����![]() ����4����
����4����
��������
��1����A��5��0���͵�B����3����4������y=ax2+bx+2��������⣻
��2��C������Ϊ��0��2�����ѵ�B��C���������ֱ�߷���y=kx+b������⣻
��3����AEֱ�ߵ�б��kAE=2����ֱ��BCб�ʵ�kAE=2������⣻
�ڿ��ǵ�P�����߶�BC��ʱ�����߶�BE��ʱ�������������PM��=PM������⣮
��1����A��5��0���͵�B����3����4������y=ax2+bx+2��
��ã�a=��![]() ��b=
��b=![]() ��
��
�ʺ����ı���ʽΪy=��![]() x2+
x2+![]() x+2��
x+2��
��2��C������Ϊ��0��2�����ѵ�B��C���������ֱ�߷���y=kx+b��
��ã�k=2��b=2��
�ʣ�ֱ��BC�ĺ�������ʽΪy=2x+2��
��3����E�ǵ�B����y��ĶԳƵ㣬E����Ϊ��3����4����
��AEֱ�ߵ�б��kAE=2����ֱ��BCб�ʵ�kAE=2��
��AE��BC����EP��BC����BP��AE
��BP=AE�����߶�BP���߶�AE�Ĺ�ϵ�����ֱ��
�����P�ĺ�����Ϊm��
��P�����߶�BC��ʱ��
P������m��2m+2����M������m��2������PM=2m��
ֱ��MM����BC����kMM��=��![]() ��
��
ֱ��MM��ķ���Ϊ��y=��![]() x+��2+
x+��2+![]() m����
m����
��M��������0��2+![]() m����4+m��0����
m����4+m��0����
������ã�PM��=PM=2m��
PM��2=42+![]() m2=��2m��2����ʽ��������
m2=��2m��2����ʽ��������
��PM��2=m2+��2m+2��2=��2m��2��
��ã�m=��4��2![]() ��
��
�ʵ�P������Ϊ����4��2![]() ����8��4
����8��4![]() ����
����
��P�����߶�BE��ʱ��
��P������m����4������M������m��2����
��PM=6��
ֱ��MM��ķ��̲��䣬Ϊy=��![]() x+��2+
x+��2+![]() m����
m����
��M��������0��2+![]() m����4+m��0����
m����4+m��0����
PM��2=m2+��6+![]() m��2=��2m��2��
m��2=��2m��2��
��ã�m=0����![]() ��
��
��PM��2=42+42=��6��2���⣻
�ʵ�P������Ϊ��0����4����![]() ����4����
����4����
����������
��P������������4+2![]() ����8+4
����8+4![]() ����4��2
����4��2![]() ����8��4
����8��4![]() ����0����4����
����0����4����![]() ����4����
����4����

 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д� һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�