题目内容
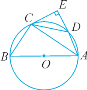
【题目】如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,连接CD且DC=BC,过C点作AD的垂线交AD延长线于E.
(1)求证:CE是⊙O的切线;
(2)若AB=5,AC=4,求tan∠DCE的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OC,OA=OC,则∠OCA=∠OAC,再由已知条件,可得∠ODE=90°;
(2)由CE是⊙O的切线,得∠DCE=∠CAE=∠CAB,从而求得tan∠DCE的值.

(1)证明:连接OC,
∵OA=OC,
∴∠OCA=∠OAC,
∵DC=BC,
∴![]() ,
,
∴∠BAC=∠CAD,
∴∠OCA=∠CAD,
∵∠CAD+∠ACE=90°,∠ACE+∠ACO=90°,
∴OC⊥CE,
∴CE是⊙O的切线.
(2)∵CE是⊙O的切线,
∴∠DCE=∠CAE,
∵BD=CD,
∴∠CAE=∠CAB,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=5,AC=4,
∴BC=3,
∴![]() .
.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目