题目内容
【题目】如图①，在△ABC中，∠ABC与∠ACB的平分线相交于点P．
（1）如果∠A=80°，求∠BPC的度数；
（2）如图②，作△ABC外角∠MBC，∠NCB的角平分线交于点Q，试探索∠Q、∠A之间的数量关系．
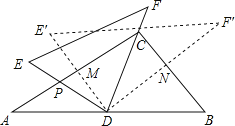
（3）如图③，延长线段BP、QC交于点E，△BQE中，存在一个内角等于另一个内角的2倍，求∠A的度数.
【答案】（1）∠P=130°；（2）∠Q=90°-
∠A；（3）∠A=60°、120°、90°
【解析】试题分析：（1）运用三角形的内角和定理及角平分线的定义，首先求出∠1+∠2，进而求出∠BPC即可解决问题；
（2）根据三角形的外角性质分别表示出∠MBC与∠BCN，再根据角平分线的性质可求得∠CBQ+∠BCQ，最后根据三角形内角和定理即可求解；
（3）在△BQE中，由于∠Q=90°﹣
∠A，求出∠E=
∠A，∠EBQ=90°，所以如果△BQE中，存在一个内角等于另一个内角的2倍，那么分四种情况进行讨论：①∠EBQ=2∠E=90°；②∠EBQ=2∠Q=90°；③∠Q=2∠E；④∠E=2∠Q；分别列出方程，求解即可．
试题解析：（1）如图①，∵在△ABC中，∠A+∠ABC+∠ACB=180°，且∠A=80°，∴∠ABC+∠ACB=100°，∵∠1=
∠ABC，∠2=
∠ACB，∴∠1+∠2=
（∠ABC+∠ACB）=
×100°=50°，∴∠BPC=180°﹣（∠1+∠2）=180°﹣50°=130°．
（2）如图②，∵∠MBC=∠A+∠ACB，∠BCN=∠ABC+∠A，∴∠MBC+∠BCN=∠A+∠ABC+∠ACB+∠A=180°+∠A．
∵BE，CQ分别为△ABC的外角∠MBC，∠NCB的角平分线，∴∠CBQ+∠BCQ=
（180°+∠A），∴∠Q=180°﹣（∠CBQ+∠BCQ）=90°﹣
∠A；
（3）如图③，连结BC并延长到点F．
∵CQ为△ABC的外角∠NCB的角平分线，∴CE是△ABC的外角∠ACF的平分线，∴∠ACF=2∠ECF，∵BE平分∠ABC，∴∠ABC=2∠EBC，∵∠ECF=∠EBC+∠E，∴2∠ECF=2∠EBC+2∠E，即∠ACF=∠ABC+2∠E，又∵∠ACF=∠ABC+∠A，∴∠A=2∠E，即∠E=
∠A；
∵∠EBQ=∠EBC+∠CBQ
=
∠ABC+
∠MBC
=
（∠ABC+∠A+∠ACB）=90°．
如果△BQE中，存在一个内角等于另一个内角的2倍，那么分四种情况：
①∠EBQ=2∠E=90°，则∠E=45°，∠A=2∠E=90°；
②∠EBQ=2∠Q=90°，则∠Q=45°，∠E=45°，∠A=2∠E=90°；
③∠Q=2∠E，则90°﹣
∠A=∠A，解得∠A=60°；
④∠E=2∠Q，则
∠A=2（90°﹣
∠A），解得∠A=120°．
综上所述，∠A的度数是90°或60°或120°．
