题目内容
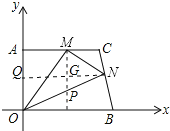
【题目】在平面直角坐标系中,直角梯形AOBC的位置图所示,∠OAC=90°,AC∥OB,OA=4,AC=5,OB=6.M、N分别在线段AC、线段BC上运动,当△MON的面积达到最大时,存在一种使得△MON周长最小的情况,则此时点M的坐标为 .

【答案】M(3,4).
【解析】
试题分析:过点M作MP∥OA,交ON于点P,过点N作NQ∥OB,分别交OA、MP于两点Q、G,则S△MON=S△OMP+S△NMP=![]() MPQG+
MPQG+![]() MPNG=
MPNG=![]() MPQN,因为QN取得最大值是QN=OB时,△MON的面积最大值=
MPQN,因为QN取得最大值是QN=OB时,△MON的面积最大值=![]() OAOB,设O关于AC的对称点D,连接DB,交AC于M,此时△OMN面积最大,周长最小.
OAOB,设O关于AC的对称点D,连接DB,交AC于M,此时△OMN面积最大,周长最小.
解:如图,过点M作MP∥OA,交ON于点P,过点N作NQ∥OB,分别交OA、MP于两点Q、G,
则S△MON=S△OMP+S△NMP=![]() MPQG+
MPQG+![]() MPNG=
MPNG=![]() MPQN,
MPQN,
∵MP≤OA,QN≤OB,
∴当点N与点B重合,QN取得最大值OB时,△MON的面积最大值=![]() OAOB,
OAOB,
设O关于AC的对称点D,连接DB,交AC于M,
此时△MON的面积最大,周长最短,
∵AM∥BO
∴![]() =
=![]() ,即
,即![]() =
=![]()
∴AM=3,
∴M(3,4).

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目