题目内容
【题目】设O是等边三角形ABC内一点,已知∠AOB=130°,∠BOC=125°,则在以线段OA,OB,OC为边构成的三角形中,内角不可能取到的角度是( )
A.65° B.60° C.45° D.70°
【答案】B
【解析】
试题分析:以B为中心,将△BOA逆时针方向旋转60°,则点A落在点C上,点O落在点D上,连接OD,找出△COD即为以线段OA,OB,OC为边构成的三角形,再由角与角之间的关系即可得出结论.
解:以B为中心,将△BOA逆时针方向旋转60°,则点A落在点C上,点O落在点D上,连接OD,如图所示.
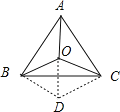
∵OB=BD,∠OBD=60°,
∴△BOD是等边三角形,
∴OD=OB,
又∵CD=OA,
故△COD是以OA,OB,OC为边构成的一个三角形.
∵∠BOC=125°,∠BOD=60°,
∴∠COD=65°;
又∵∠BDC=∠AOB=130°,∠BDO=60°,
∴∠ODC=70°;
从而∠OCD=180°﹣65°﹣70°=45°.
故求得以线段OA,OB,OC为边构成的三角形的各角为65°,70°,45°.
故选B.

练习册系列答案
相关题目