Question

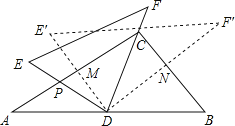
【题目】将一副三角尺（在Rt△ABC中，∠ACB=90°，∠B=60°，在Rt△EDF中，∠EDF=90°，∠E=45°）如图摆放，点D为AB的中点，DE交AC于点P，DF经过点C，将△EDF绕点D顺时针方向旋转α（0°＜α＜60°），DE′交AC于点M，DF′交BC于点N，则的值为（ ）

A． B． C． D．

Answer 1

【答案】C

【解析】

试题分析：先根据直角三角形斜边上的中线性质得CD=AD=DB，则∠ACD=∠A=30°，∠BCD=∠B=60°，由于∠EDF=90°，可利用互余得∠CPD=60°，再根据旋转的性质得∠PDM=∠CDN=α，于是可判断△PDM∽△CDN，得到=，然后在Rt△PCD中利用正切的定义得到tan∠PCD=tan30°=，于是可得=．

解：∵点D为斜边AB的中点，

∴CD=AD=DB，

∴∠ACD=∠A=30°，∠BCD=∠B=60°，

∵∠EDF=90°，

∴∠CPD=60°，

∴∠MPD=∠NCD，

∵△EDF绕点D顺时针方向旋转α（0°＜α＜60°），

∴∠PDM=∠CDN=α，

∴△PDM∽△CDN，

∴=，

在Rt△PCD中，∵tan∠PCD=tan30°=，

∴=tan30°=．

故选C．