题目内容
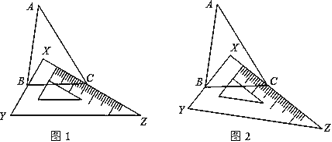
【题目】(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C直角顶点X在△ABC内部,若∠A=30,则∠ABC+∠ACB=_____,∠XBC+∠XCB=________
(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C,直角顶点X还在△ABC内部,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
【答案】(1) 150°,90°;(2)60°.
【解析】
在△ABC中,利用三角形内角和等于180°,可求∠ABC+∠ACB=180°-∠A,即可求∠ABC+∠ACB;同理在△XBC中,∠BXC=90°,那么∠XBC+∠XCB=180°-∠BXC,即可求∠XBC+∠XCB;(2)不发生变化,由于在△ABC中,∠A=30°,从而∠ABC+∠ACB是一个定值,即等于150°,同理在△XBC中,∠BXC=90°,那么∠XBC+∠XCB也是一个定值,等于90°,于是∠ABX+∠ACX的值不变,等于150°-90°=60°;
(1)∵∠A+∠ABC+∠ACB=180°,∠A=30°,
∴∠ABC+∠ACB=180°-30°=150°,
同理可得:∠XBC+∠XCB=180°-90°=90°,
故答案为:150°,90°
(2)不发生变化.
∵∠A=30°,
∴∠ABC+∠ACB=180°-∠A=150°,(三角形内角和180°)
∵∠YXZ=90°,
∴∠XBC+∠XCB=90°,(三角形内角和180°)
∴∠ABX+∠ACX=150°-90°=60°.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目