题目内容
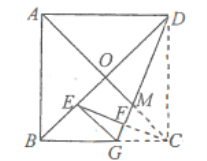
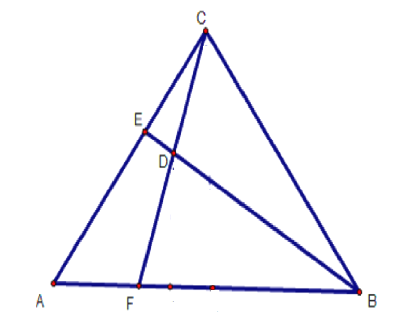
【题目】如图,![]() 中,
中,![]() ,则
,则![]() ____.
____.
【答案】2![]()
【解析】
如下图,先推导出∠DFB=60°,并得出△ECD∽△FBD,设FG=a,则利用相似,可得出FB的大小,从而得出GB的长,然后再Rt△DGB中,得出DB的长,从而得出CB的长,最后在Rt△CHB中,利用勾股定理求出a的值,进而得出AF的长.
如下图,过点D、C作AB的垂线,分别交AB于点G、H
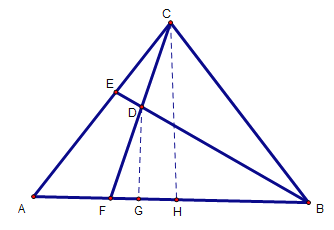
∵BD=BC=AC,∴∠CDB=∠DCB
∵∠ACB+∠CBD=120°,∠CDB+∠DCB+∠CBD=180°
∴∠ACF+∠DCB+∠CBD=120°
∴∠CDB=∠ACF+60°
设∠ACF=x,则∠DCB=∠CDB=x+60
∴∠CAB=∠CBA=60-x,∠CBE=60-2x,∠EBA=x
∴∠CFB=∠ACF+∠CAF=60°
∵∠ECD=∠DBF=x,∠CDE=∠BDF
∴△ECD∽△FBD
设FG=a
则在Rt△FGD中,FD=2a,DG=![]()
∵△ECD∽△FBD,CE=3,ED=1
∴![]()
解得:FB=6a
∴GB=5a
∴在Rt△DBG中,DB=2![]() a=BC
a=BC
∵![]()
∴CD=2![]()
∴在Rt△CFH中,FH=![]() ,CH=
,CH=![]()
∴GH=![]() ,HB=5a-
,HB=5a-![]()
∵AC=BC
∴AH=BH=5a-![]()
∴AF=AH-FG-GH=5a-![]() =4a-2
=4a-2![]()
在Rt△CHB中,![]() ,即
,即![]()
解得;a=![]()
∴AF=4a-2![]() =4
=4![]()
故答案为:2![]() .
.

练习册系列答案
相关题目