题目内容
【题目】大数学家欧拉非常推崇观察能力,他说过,今天已知的许多数的性质,大部分是通过观察发现的,历史上许多大家,都是天才的观察家,化归就是将面临的新问题转化为已经熟悉的规范问题的数学方法,这是一种具有普遍适用性的数学思想方法.如多项式除以多项式可以类比于多位数的除法进行计算:
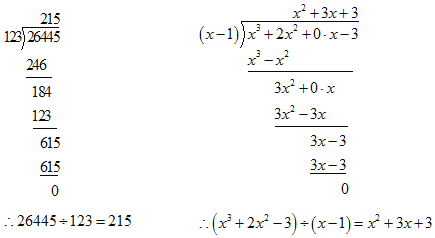
请用以上方法解决下列问题:
(1)计算:(x3+2x2﹣3x﹣10)÷(x﹣2);
(2)若关于x的多项式2x4+5x3+ax2+b能被二项式x+2整除,且a,b均为自然数,求满足以上条件的a,b的值及相应的商.
【答案】(1)x2+4x+5;(2)当a=0,b=8时,此时多项式为2x4+5x3+8,商为2x3+x2﹣2x+4;当a=1,b=4时,此时多项式为2x4+5x3+x2+4,商为2x3+x2﹣x+2
【解析】
(1)直接利用竖式计算即可;
(2)竖式计算,根据整除的意义,利用对应项的系数对应倍数求得答案即可.
解:(1)列竖式如下:
![]()

(x3+2x2﹣3x﹣10)÷(x﹣2)=x2+4x+5;
(2)列竖式如下:

∵多项式2x4+5x3+ax2+b能被二项式x+2整除,
∴余式b+4(a﹣2)=0,
∵a,b均为自然数,
∴当a=0,b=8时,此时多项式为2x4+5x3+8,商为2x3+x2﹣2x+4,
当a=1,b=4时,此时多项式为2x4+5x3+x2+4,商为2x3+x2﹣x+2,
当a=2,b=0时,此时多项式为2x4+5x3+2x2,商为2x3+x2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目