题目内容
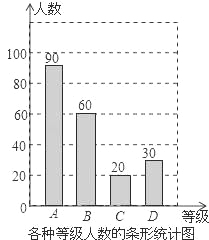
【题目】某中学积极组织学生开展课外阅读活动,为了解本校学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:

(1)求出x的值,并将不完整的条形统计图补充完整;
(2)若该校共有学生2500人,试估计每周课外阅读时间量满足2≤t<4的人数;
(3)若本次调查活动中,九年级(1)班的两个学习小组分别有3人和2人每周阅读时间量都在4小时以上,现从这5人中任选2人参加学校组织的知识抢答赛,求选出的2人来自不同小组的概率.
【答案】(1)30;(2)1000人;(3)![]() .
.
【解析】试题分析:(1)根据所有等级的百分比的和为1,则可计算出x=30,再利用A等级的人数除以它所占的百分比得到调查的总人数为200人,然后分别乘以30%和20%得到B等级和C等级人数,再将条形统计图补充完整;
(2)满足2≤t<4的人数就是B和C等级的人数,用2500乘以B、C两等级所占的百分比的和即可;
(3)3人学习组的3个人用甲表示,2人学习组的2个人用乙表示,画树状图展示所有20种等可能的结果数,其中选出的2人来自不同小组占12种,然后利用概率公式求解.
试题解析:(1)∵x%+15%+10%+45%=1,
∴x=30;
∵调查的总人数=90÷45%=200(人),
∴B等级人数=200×30%=60(人);C等级人数=200×10%=20(人),
如图:
(2)2500×(10%+30%)=1000(人),
所以估计每周课外阅读时间量满足2≤t<4的人数为1000人;
(3)3人学习组的3个人用甲表示,2人学习组的2个人用乙表示,画树状图为:
 ,
,
共有20种等可能的结果数,其中选出的2人来自不同小组占12种,
所以选出的2人来自不同小组的概率=![]() .
.