Question

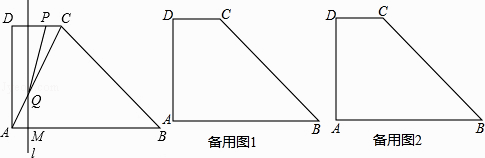
【题目】如图，直线y=x+1与y轴交于点A1 ， 依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn﹣1 ， 使得点A1、A2、…，An在直线x+1上，点C1、C2、…，Cn在x轴上，则点Bn的坐标是（ ）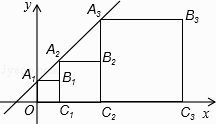

A.（2n﹣1，2n﹣1）
B.（2n﹣1+1，2n﹣1）
C.（2n﹣1，2n﹣1）
D.（2n﹣1，n）

Answer 1

【答案】A
【解析】解：∵令x=0，则y=1，
∴A1（0，1），
∴OA1=1．
∵四边形A1B1C1O是正方形，
∴A1B1=1，
∴B1（1，1）．
∵当x=1时，y=1+1=2，
∴B2（3，2）；
同理可得，B3（7，4）；
∴B1的纵坐标是：1=20 ， B1的横坐标是：1=21﹣1，
∴B2的纵坐标是：2=21 ， B2的横坐标是：3=22﹣1，
∴B3的纵坐标是：4=22 ， B3的横坐标是：7=23﹣1，
∴Bn的纵坐标是：2n﹣1 ， 横坐标是：2n﹣1，
则Bn（2n﹣1，2n﹣1）．
故选A．