Question

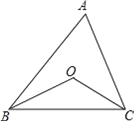
【题目】如图，已知点O是△ABC的两条角平分线的交点，

（1）若∠A=30°，则∠BOC的大小是　 　；

（2）若∠A=60°，则∠BOC的大小是　 　；

（3）若∠A=n°，则∠BOC的大小是多少？试用学过的知识说明理由．

Answer 1

【答案】 (1) 105°; (2) 120°;(3) n°+90°.

【解析】试题分析：∠BOC+∠OBC+∠OCB=180°，根据角平分线的定义得到∠ABC=2∠OBC，∠ACB=2∠OCB，等量代换得到∠BOC+ ∠ABC+∠ACB=180°，根据三角形的内角和定理即可得到结论.

试题解析：

（1）如图，在△ABC中，∠A+∠ABC+∠ACB=180°，
在△BOC中，∠BOC+∠OBC+∠OCB=180°，
∵BO，CO分别是∠ABC和∠ACB的平分线，
∴∠ABC=2∠OBC，∠ACB=2∠OCB，
∴∠BOC+ ∠ABC+∠ACB=180°，
又∵在△ABC中，∠A+∠ABC+∠ACB=180°，
∴∠BOC=∠A+90°=105°；
（2）如图，在△ABC中，∠A+∠ABC+∠ACB=180°，
在△BOC中，∠BOC+∠OBC+∠OCB=180°，
∵BO，CO分别是∠ABC和∠ACB的平分线，
∴∠ABC=2∠OBC，∠ACB=2∠OCB，
∴∠BOC+∠ABC+∠ACB=180°，
又∵在△ABC中，∠A+∠ABC+∠ACB=180°，
∴∠BOC=∠A+90°=120°；

（3）∠BOC=n°+90°，

∵OB、OC是两条角平分线，

∴∠OBC=∠ABC, ∠OCB=∠ACB ，

在△OBC中，∠BOC=180°-（∠OBC+∠OCB）

=180°-（∠ABC+∠ACB）

=180°-（∠ABC+∠ACB）

=180°-（180°-∠A）

=∠A+90°

=n°+90°.