��Ŀ����
����Ŀ����֪��ƽ��ֱ������ϵxOy�У�������y1=ax2+bx��a��0������x�������ύ�ڵ�A1��2��0��������ΪP1 �� ��OP1A1Ϊ�������Σ��ֽ�������y1=ax2+bx��a��0��������OP1ƽ�ƣ��ѹ���A1ʱ��������Ϊ������y2 �� ��������y2��x�����һ����ΪA2����������y2����������OP1ƽ�ƣ��ѹ���A2ʱ��������Ϊ������y3 �� ��������y3��x�����һ����ΪA3����������������y2015����������OP1ƽ�ƣ��ѹ���A2015ʱ��������Ϊ������y2016 �� ��������y2016��x�����һ����ΪA2016 �� ����ΪP2016 �� ����2016�������ߵĶ��㶼������OP1�ϣ�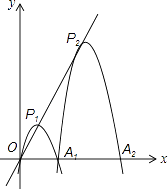
��1�������OP1A1�����������a��b��ֵ��
��2����������y2�Ľ���ʽ��
��3����ֱ��д����A2016�Լ���P2016���꣮
���𰸡�
��1��
�⣺�ٹ���P1����P1B1��x�ᣬ����ΪB1��

�ߡ�OP1A1Ϊ�������Σ�
���P1OA1=60�㣬P1O=P1A1��
�֡�P1B1��x�ᣬ
��0B1=B1A1=1��
��P1B1=OP1�� ![]() =2��
=2�� ![]() =
= ![]() ��
��
��P1��1�� ![]() ������OP1A1�����=
������OP1A1�����= ![]() OA1P1B1=
OA1P1B1= ![]() ��2��
��2�� ![]() =
= ![]() ��
��
�ڡ߽���A1��2��0����P1��1�� ![]() ����������y1�ϣ�
����������y1�ϣ�
�� ![]() ����ã�a=��
����ã�a=�� ![]() ��b=2
��b=2 ![]()
��2��
�⣺��ֱ��OP1�Ľ���ʽΪy=kx��
�߽�P1��1�� ![]() ������ã�k=
������ã�k= ![]() ��
��
��ֱ��OP1�Ľ���ʽΪy= ![]() x��
x��
�ߵ�P2��ֱ��OP1�ϣ�
�����P2��a�� ![]() ����
����
��y2=�� ![]() ��x��a��2+
��x��a��2+ ![]() a��
a��
�߽���A1���������ã��� ![]() ��2��a��2+
��2��a��2+ ![]() a=0����ã�a1=1����ȥ����a2=4��
a=0����ã�a1=1����ȥ����a2=4��
��y2=�� ��x��4��2+4
![]() �������ã�y2=��
�������ã�y2=�� ![]() x2+8
x2+8 ![]() x��12
x��12 ![]()
��3��
�⣺��a2=4��
��P2��4��4 ![]() ����
����
���A1��D��A2����x=4�Գƣ�
���A2��6��0����
��P3��b�� ![]() ����y3=��
����y3=�� ![]() ��x��b��2+
��x��b��2+ ![]() b��
b��
�߽�A2��6��0������é� ![]() ��6��b��2+
��6��b��2+ ![]() b=0����ã�b1=4����ȥ����b2=9��
b=0����ã�b1=4����ȥ����b2=9��
��P3��9��9 ![]() ����
����
��A2��6��0������A2��A3����x=9�Գƣ�
��A3��12��0����
P1��1�� ![]() ����A1��2��0����
����A1��2��0����
P2��4��4 ![]() ����A2��6��0����4=22��6=2��3��
����A2��6��0����4=22��6=2��3��
P3��9��9 ![]() ����A3��12��0����9=32��12=3��4��
����A3��12��0����9=32��12=3��4��
��
P2016��4064256��4064256 ![]() ����A2016��4066272��0��
����A2016��4066272��0��
����������1���ٹ���P1����P1B1��x�ᣬ����ΪB1 �� �ɵȱ������ε����ʿ�֪�����P1B1�ij��ȣ�Ȼ�����������ε������ʽ����á�OP1A1��������ڽ���A1��2��0����P1��1�� ![]() �����������ߵĽ���ʽ���������a��b��ֵ����2�������ô���ϵ�������ֱ��OP1�Ľ���ʽ��Ȼ�����P2��a��
�����������ߵĽ���ʽ���������a��b��ֵ����2�������ô���ϵ�������ֱ��OP1�Ľ���ʽ��Ȼ�����P2��a�� ![]() ������y2=��
������y2=�� ![]() ��x��a��2+
��x��a��2+ ![]() a��������������A1�������������a��ֵ���Ӷ��ɵõ������ߵĽ���ʽ����3����a2=4������õ�P2��4��4
a��������������A1�������������a��ֵ���Ӷ��ɵõ������ߵĽ���ʽ����3����a2=4������õ�P2��4��4 ![]() ����Ȼ�����������ߵĶԳ��Կ���õ�A2��6��0�����������������P3��9��9
����Ȼ�����������ߵĶԳ��Կ���õ�A2��6��0�����������������P3��9��9 ![]() ����A3��12��0�������۲����ý���ҳ����еĹ��ɣ����ݹ��ɿ��������Ĵ𰸣�
����A3��12��0�������۲����ý���ҳ����еĹ��ɣ����ݹ��ɿ��������Ĵ𰸣�
�����㾫����ͨ�������������ʽ�Ĺ��ɣ������ȴ�ͼ����Ѱ�ҹ��ɣ�Ȼ����֤���ɣ�Ӧ�ù��ɣ������ν��Ѱ�ҹ��ɼ����Խ����⣮

 �ǻۿ����ܾ�100�ֵ�Ԫ���ؼ��ϵ�д�
�ǻۿ����ܾ�100�ֵ�Ԫ���ؼ��ϵ�д�����Ŀ��ij���ڳ��д�����У���Ҫ��ֲ![]() ��
��![]() ���ֲ�ͬ�����繲
���ֲ�ͬ�����繲![]() �ã����б꣬�а�����
�ã����б꣬�а�����![]() ��Ԫ�ı����б�а�������̣����ݵ��鼰������ϱ�����
��Ԫ�ı����б�а�������̣����ݵ��鼰������ϱ����� ![]() ��
��![]() ��������ijɱ��ۼ��ɻ��������
��������ijɱ��ۼ��ɻ��������
Ʒ�� | ����ۣ�Ԫ/�ã� | �ɻ��� |
|
|
|
|
|
|
����ֲ![]() ������
������![]() �ã��а��̻�õ�����Ϊ
�ã��а��̻�õ�����Ϊ![]() Ԫ��
Ԫ��
��![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��![]() ������Ҫ����ֲ��������ijɻ��ʲ�����
������Ҫ����ֲ��������ijɻ��ʲ�����![]() ���а���Ӧ���ѡ��������ܻ�����������������Ƕ��٣�
���а���Ӧ���ѡ��������ܻ�����������������Ƕ��٣�