题目内容
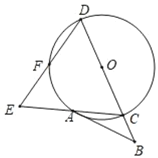
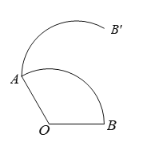
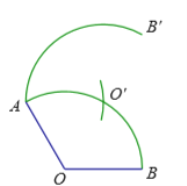
【题目】如图，将圆心角为120°的扇形AOB绕着点A按逆时针方向旋转一定的角度后，得到扇形AO′B′，使得点O′ 恰
在上．
（1）求作点O′；(尺规作图，保留作图痕迹，不写作法和证明过程)
（2）连接AB、AB'、AO′，求证：AO′平分∠BAB′．
【答案】（1）见解析；（2）证明见解析
【解析】
（1如图所示：连接
，作的线段垂直平分线
，则直线与
的交点
即为所求作的点（方法不唯一）；
（2）由旋转的性质可得
，进而证得
是等边三角形，由此推出旋转角为
，再由旋转的性质可得
，由三角形内角和定理可知∠OAB＝∠OBA＝30°，继而由角的和差计算得
，
，
最后即可求出结论．
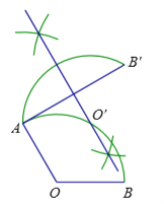
解：
解法一：如图点是所求作的点
(或在
上任取不同的点
，连接
，作的中垂线，则直线与的交点即为所求作的点，图略)
解法二：如图点是所求作的点
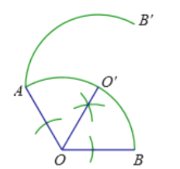
解法三：如图点是所求作的点
证明：连接
由旋转的性质可得
又
，即是等边三角形．
，即旋转角为
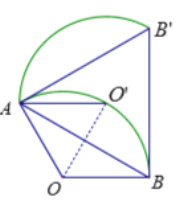
由旋转的性质可得
，
，
即
平分
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
