题目内容
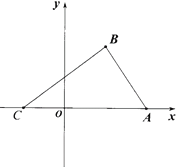
【题目】如图,在平面直角坐标系中,已知△ABC,点A的坐标是(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.
(1)直接写出点C的坐标.
(2)在y轴上是否存在点P,使得S△POB=![]() S△ABC若存在,求出点P的坐标;若不存在,请说明理由.
S△ABC若存在,求出点P的坐标;若不存在,请说明理由.
(3)把点C往上平移3个单位得到点H,作射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探究∠HBM,∠BMA,∠MAC之间的数量关系,并证明你的结论.
【答案】(1)C(-2,0);(2)点P坐标为(0,6)或(0,-6);(3)∠BMA=∠MAC±∠HBM,证明见解析.
【解析】
(1)由点A坐标可得OA=4,再根据C点x轴负半轴上,AC=6即可求得答案;
(2)先求出S△ABC=9,S△BOP=OP,再根据S△POB=![]() S△ABC,可得OP=6,即可写出点P的坐标;
S△ABC,可得OP=6,即可写出点P的坐标;
(3)先得到点H的坐标,再结合点B的坐标可得到BH//AC,然后根据点M在射线CH上,分点M在线段CH上与不在线段CH上两种情况分别进行讨论即可得.
(1)∵A(4,0),
∴OA=4,
∵C点x轴负半轴上,AC=6,
∴OC=AC-OA=2,
∴C(-2,0);
(2)∵B(2,3),
∴S△ABC=![]() ×6×3=9,S△BOP=
×6×3=9,S△BOP=![]() OP×2=OP,
OP×2=OP,
又∵S△POB=![]() S△ABC,
S△ABC,
∴OP=![]() ×9=6,
×9=6,
∴点P坐标为(0,6)或(0,-6);
(3)∠BMA=∠MAC±∠HBM,证明如下:
∵把点C往上平移3个单位得到点H,C(-2,0),
∴H(-2,3),
又∵B(2,3),
∴BH//AC;
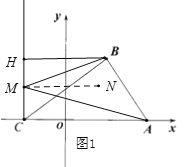
如图1,当点M在线段HC上时,过点M作MN//AC,
∴∠MAC=∠AMN,MN//HB,
∴∠HBM=∠BMN,
∵∠BMA=∠BMN+∠AMN,
∴∠BMA=∠HBM+∠MAC;
如图2,当点M在射线CH上但不在线段HC上时,过点M作MN//AC,
∴∠MAC=∠AMN,MN//HB,
∴∠HBM=∠BMN,
∵∠BMA=∠AMN-∠BMN,
∴∠BMA=∠MAC-∠HBM;
综上,∠BMA=∠MAC±∠HBM.


 每课必练系列答案
每课必练系列答案