题目内容
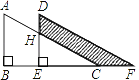
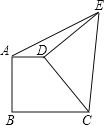
【题目】如图直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，BC=3，将腰CD以D为中心逆时针旋转90°至ED，连AE、CE，则△ADE的面积是（ ）
A. 1 B. 2 C. 3 D. 不能确定
【答案】A
【解析】如图作辅助线，利用旋转和三角形全等证明△DCG与△DEF全等，再根据全等三角形对应边相等可得EF的长，即△ADE的高，然后得出三角形的面积．
如图所示，作EF⊥AD交AD延长线于F，作DG⊥BC，
∵CD以D为中心逆时针旋转90°至ED，
∴∠EDF+∠CDF=90°，DE=CD，
又∵∠CDF+∠CDG=90°，
∴∠CDG=∠EDF，
在△DCG与△DEF中，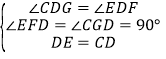
，
∴△DCG≌△DEF（AAS），
∴EF=CG，
∵AD=2，BC=3，
∴CG=BC﹣AD=3﹣2=1，
∴EF=1，
∴△ADE的面积是：
×AD×EF=×2×1=1，
故选A．
全优考典单元检测卷及归类总复习系列答案
【题目】某年5月，我国南方某省A、B两市遭受严重洪涝灾害，1.5万人被迫转移，邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后，决定调运物资支援灾区．已知C市有救灾物资240吨，D市有救灾物资260吨，现将这些救灾物资全部调往A、B两市．已知从C市运往A、B两市的费用分别为每吨20元和25元，从D市运往往A、B两市的费用别为每吨15元和30元，设从D市运往B市的救灾物资为x吨．
（1）请填写下表
A（吨） | B（吨） | 合计（吨） | |
C |
|
| 240 |
D |
| x | 260 |
总计（吨） | 200 | 300 | 500 |
（2）设C、D两市的总运费为w元，求w与x之间的函数关系式，并写出自变量x的取值范围；
（3）经过抢修，从D市到B市的路况得到了改善，缩短了运输时间，运费每吨减少m元（m＞0），其余路线运费不变．若C、D两市的总运费的最小值不小于10320元，求m的取值范围．
