题目内容
【题目】如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= °;
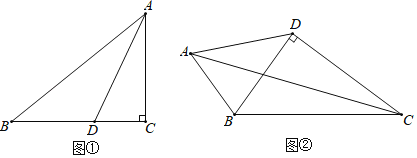
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
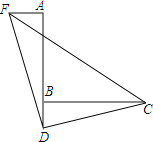
(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.
【答案】(1)15°;(2)BE=![]() .(3)AC=20.
.(3)AC=20.
【解析】
(1)根据“准互余三角形”的定义构建方程即可解决问题;
(2)只要证明△CAE∽△CBA,可得CA2=CECB,由此即可解决问题;
(3)如图②中,将△BCD沿BC翻折得到△BCF.只要证明△FCB∽△FAC,可得CF2=FBFA,设FB=x,则有:x(x+7)=122,推出x=9或﹣16(舍弃),再利用勾股定理求出AC即可;
(1)∵△ABC是“准互余三角形”,∠C>90°,∠A=60°,
∴2∠B+∠A=60°,
解得,∠B=15°;
(2)如图①中,
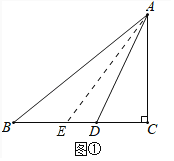
在Rt△ABC中,∵∠B+∠BAC=90°,∠BAC=2∠BAD,
∴∠B+2∠BAD=90°,
∴△ABD是“准互余三角形”,
∵△ABE也是“准互余三角形”,
∴只有2∠B+∠BAE=90°,
∵∠B+∠BAE+∠EAC=90°,
∴∠CAE=∠B,∵∠C=∠C=90°,
∴△CAE∽△CBA,可得CA2=CECB,
∴CE=![]() ,
,
∴BE=5﹣![]() =
=![]() .
.
(3)如图②中,将△BCD沿BC翻折得到△BCF.
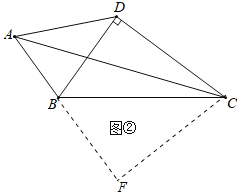
∴CF=CD=12,∠BCF=∠BCD,∠CBF=∠CBD,
∵∠ABD=2∠BCD,∠BCD+∠CBD=90°,
∴∠ABD+∠DBC+∠CBF=180°,
∴A、B、F共线,
∴∠A+∠ACF=90°
∴2∠ACB+∠CAB≠90°,
∴只有2∠BAC+∠ACB=90°,
∴∠FCB=∠FAC,∵∠F=∠F,
∴△FCB∽△FAC,
∴CF2=FBFA,设FB=x,
则有:x(x+7)=122,
∴x=9或﹣16(舍去),
∴AF=7+9=16,
在Rt△ACF中,AC=![]() .
.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案【题目】已知多项式4x6y2- 3x2y- x- 7,次数是b,4a与b互为相反数,在数轴上,点A表示数a,点B表示数b.
(1)a=____________,b=____________
(2)若小蚂蚁甲从点A处以3个单位长度/秒的速度向左运动,同时小蚂蚁乙从点B处以4单位长度/秒的速度也向左运动,丙同学观察两只小蚂蚁运动,在它们刚开始运动时,在原点0处放置一颗饭粒,乙在碰到饭粒后立即背着饭粒以原来的速度向相反的方向运动,设运动的时间为t秒,求甲、乙两只小蚂蚁到原点的距离相等时所对应的时间t.(写出解答过程)
(3)若小蚂蚁甲和乙约好分别从A,B两点,分别沿数轴甲向左,乙向右以相同的速度爬行,经过一段时间原路返回,刚好在16s时一起重新回到原出发点A和B,设小蚂蚁们出发t(s)时的速度为v(mm/s),v与t之间的关系如下图.(其中s表示时间单位秒,mm表示路程单位毫米)
t (s) | 0<t≤2 | 2<t≤5 | 5<t≤16 |
v(mm/s) | 10 | 16 | 8 |
①当2<t≤5时,你知道小蚂蚁甲与乙之间的距离吗?(用含有t的代数式表示);
②当t为__________________时,小蚂蚁甲乙之间的距离是42mm.(请直接写出答案)
![]()