题目内容
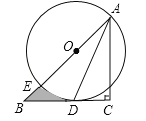
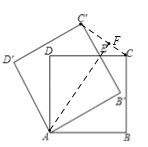
【题目】如图,将正方形ABCD绕点A逆时针旋转30°得到AB′C′D′,如果AB=1,点C与C′的距离为( )

A. ![]() B.
B. ![]() ﹣
﹣![]() C. 1 D.
C. 1 D. ![]() ﹣1
﹣1
【答案】D
【解析】
连接CC′,AE,延长AE交CC′于F,由正方形性质可证明△ADE≌△AEB′,所以DE=B′E,根据∠BAB′=30°可知∠DAE=∠EAB′=30°,即可求出DE的长度,进而求出CE的长度,根据∠FEC=60°可知CF的长度,即可求出CC′的长度.
连接CC′,AE,延长AE交CC′于F,
∵正方形ABCD绕点A逆时针旋转30°得到AB′C′D′,
∴AD=AB′,∠ADE=∠AB′E=90°,AE=AE,
∴△ADE≌△A EB′,
∴∠DAE=∠EAB′,
∵旋转角为30°,
∴∠BAB′=30°,
∴∠DAB′=60°,
∴∠DAE=∠EAB′=30°,
∴AE=2DE,
∴AD2+DE2=(2DE)2,
∴DE=![]() ,
,
∴CE=1-![]() ,
,
∵DE=EB′
∴EC=EC′,
∵∠DEA=∠AEB′=60°,
∴∠FEC′=∠FEC=60°,
∴∠FCE=30°,
∴△FEC≌△FEC′,
∴CF=FC′,
∴EF⊥CC′,
∴EF=![]() CE=
CE=![]() ,
,
∴CF=![]() =
= ![]() ,
,
∴CC′=2CF=![]() ,
,
故选D.

练习册系列答案
相关题目