题目内容
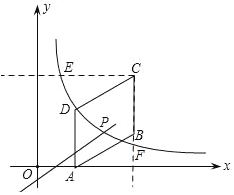
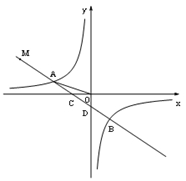
【题目】如图，四边形ABCD是平行四边形，点A（1，0），B（4，1），C（4，3），反比例函数y=
的图象经过点D，点P是一次函数y=mx+3﹣4m（m≠0）的图象与该反比例函数图象的一个公共点；
（1）求反比例函数的解析式；
（2）通过计算说明一次函数y=mx+3﹣4m的图象一定过点C；
（3）对于一次函数y=mx+3﹣4m（m≠0），当y随x的增大而增大时，确定点P的横坐标的取值范围，（不必写过程）
【答案】（1）y=
；（2）C（4，3）；（3）见解析.
【解析】试题分析：（1）由B（4，1），C（4，3）得到BC⊥x轴，BC=2，根据平行四边形的性质得AD=BC=2，而A点坐标为（1，0），可得到点D的坐标为（1，2），然后把D（1，2）代入y=
即可得到k=2，从而可确定反比例函数的解析式；
（2）把x=4代入y=mx+3﹣4m（m≠0）得到y=3，即可说明一次函数y=mx+3﹣4m（m≠0）的图象一定过点C；
（3）设点P的横坐标为x，由于一次函数y=mx+3﹣4m（m≠0）过C点，并且y随x的增大而增大时，则P点的纵坐标要小于3，横坐标要小于3，当纵坐标小于3时，由y=
得到x＞
，于是得到x的取值范围．
试题解析：解：（1）∵B（4，1），C（4，3），
∴BC∥y轴，BC=2，
又∵四边形ABCD是平行四边形，
∴AD=BC=2，AD∥y轴，而A（1，0），
∴D（1，2），
∴由反比例函数y=
的图象经过点D，可得k=1×2=2，
∴反比例函数的解析式为y=
；
（2）∵在一次函数y=mx+3﹣4m中，当x=4时，y=4m+3﹣4m=3，
∴一次函数y=mx+3﹣4m的图象一定过点C（4，3）；
（3）点P的横坐标的取值范围：
＜x＜4．
如图所示，过C（4，3）作y轴的垂线，交双曲线于E，作x轴的垂线，交双曲线于F，
当y=3时，3=，即x=，
∴点E的横坐标为；
由点C的横坐标为4，可得F的横坐标为4；
∵一次函数y=mx+3﹣4m的图象一定过点C（4，3），且y随x的增大而增大，
∴直线y=mx+3﹣4m与双曲线的交点P落在EF之间的双曲线上，
∴点P的横坐标的取值范围是＜x＜4．
