题目内容
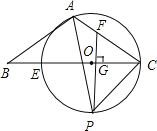
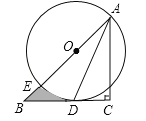
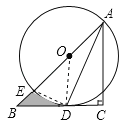
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接DE,OD.利用弦切角定理,直径所对的圆周角是直角,等角的余角相等证明∠DAO=∠CAD,进而得出结论;
(2)根据等腰三角形的性质得到∠B=∠BAC=45°,由BC相切⊙O于点D,得到∠ODB=90°,求得OD=BD,∠BOD=45°,设BD=x,则OD=OA=x,OB=![]() x,根据勾股定理得到BD=OD=
x,根据勾股定理得到BD=OD=![]() ,于是得到结论.
,于是得到结论.
试题解析:解:(1)证明:连接DE,OD.
∵BC相切⊙O于点D,∴∠CDA=∠AED,∵AE为直径,∴∠ADE=90°,∵AC⊥BC,∴∠ACD=90°,∴∠DAO=∠CAD,∴AD平分∠BAC;
(2)∵在Rt△ABC中,∠C=90°,AC=BC,∴∠B=∠BAC=45°,∵BC相切⊙O于点D,∴∠ODB=90°,∴OD=BD,∴∠BOD=45°,设BD=x,则OD=OA=x,OB=![]() x,∴BC=AC=x+1,∵AC2+BC2=AB2,∴2(x+1)2=(
x,∴BC=AC=x+1,∵AC2+BC2=AB2,∴2(x+1)2=(![]() x+x)2,∴x=
x+x)2,∴x=![]() ,∴BD=OD=
,∴BD=OD=![]() ,∴图中阴影部分的面积=S△BOD﹣S扇形DOE=
,∴图中阴影部分的面积=S△BOD﹣S扇形DOE=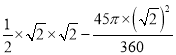 =
=![]() .
.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目