题目内容
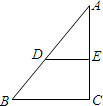（2013•闸北区一模）如图，已知点D、E分别在△ABC的边AB和AC上，且DE∥BC，S△AED：S梯形EDBC=1：2，则AE：AC的比值是
| ||
| 3 |
| ||
| 3 |
分析：由DE∥BC得△ADE∽△ABC，再根据相似三角形面积比等于相似比的平方进而求出AE：AC的比值．
解答：解：∵DE∥BC，
∴△ADE∽△ABC，
∵S△ADE：S梯形BCED=1：2，
∴S△ADE：S△ABC=1：3，
∴AE：AC=1：
=
，
故答案为：
．
∴△ADE∽△ABC，
∵S△ADE：S梯形BCED=1：2，
∴S△ADE：S△ABC=1：3，
∴AE：AC=1：
| 3 |
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考查了相似三角形的判定与性质，三角形相似的判定一直是中考考查的热点之一，在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形；或依据基本图形对图形进行分解、组合；或作辅助线构造相似三角形，判定三角形相似的方法有事可单独使用，有时需要综合运用，无论是单独使用还是综合运用，都要具备应有的条件方可．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2013•闸北区一模）已知：如图，二次函数
（2013•闸北区一模）已知：如图，在平行四边形ABCD中，对角线AC、BD相交于点O，点M、N分别在边AO和边OD上，且AM=
（2013•闸北区一模）已知：如图，在△ABC中，BD⊥AC于点D，CE⊥AB于点E，EC和BD相交于点O，联接DE．