题目内容
 (2013•闸北区一模)已知:如图,二次函数y=
(2013•闸北区一模)已知:如图,二次函数y=| 2 |
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
(1)求点E的坐标;
(2)在x轴上方找一点C,使以点C、O、B为顶点的三角形与△BOE相似,请直接写出点C的坐标.
分析:(1)根据二次函数解析式求得点B的坐标;设直线BQ:y=kx+b(k≠0).则把B、Q的坐标代入该解析式列出关于系数k、b的方程组,通过解方程组即可求得它们的值;最后令x=0,则y=-8,即E(0,-8);
(2)需要分类讨论:①如图1,若∠COB=∠EOB=90°;②如图1,若∠CBO=∠EOB=90°;③如图2,若∠OCB=∠BOE=90°.由相似三角形的对应边成比例求得相关线段的长度.
(2)需要分类讨论:①如图1,若∠COB=∠EOB=90°;②如图1,若∠CBO=∠EOB=90°;③如图2,若∠OCB=∠BOE=90°.由相似三角形的对应边成比例求得相关线段的长度.
解答:解:(1)令y=0,得
x2-
x-
=0,
解方程,得
x1=-2,x2=4,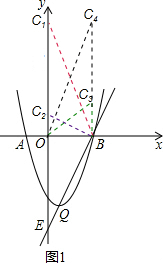
∵点A在点B的左侧,
∴B(4,0)
又y=
(x-1)2-6,
∴Q(1,-6).
设直线BQ:y=kx+b(k≠0).则把B、Q的坐标代入,得
解得
,
∴直线BQ的解析式是:y=2x-8,
∴E(0,-8);
(2)由(1)知,B(4,0),E(0,-8),则OE=8,OB=4.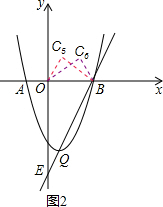
①如图1,若∠COB=∠EOB=90°.
当△BOC∽△BOE时,
=
=1,即OC=OE=8,则C1(0,8);
当△COB∽△BOE时,
=
,即
=
,则CO=2,故C2(0,2);
②如图1,若∠CBO=∠EOB=90°.
当△CBO∽△BOE时,
=
,即
=
,解得,CB=2,故C3(4,2);
当△OBC∽△BOE时,
=
=1,即BC=OE=8,故C4(4,8);
③如图2,若∠OCB=∠BOE=90°,设C(x,y).
△OCB∽△BOE时,
=
,即
=
,或
=
①.
∵直角△BOC中,根据勾股定理知OC2+BC2=OB2=16,②
∴由①②得,OC=
,BC=
OC•BC=
.
∵
OB•y=
OC•BC,
∴y=
,
∴x=
,即C5(
,
).
同理,当△BCO∽△BOE时,C6(
,
).
综上所述,符合条件的点C的坐标是:
C1(0,8),C2(0,2),C3(4,2),C4(4,8),C5(
,
),C6(
,
).
| 2 |
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
解方程,得
x1=-2,x2=4,

∵点A在点B的左侧,
∴B(4,0)
又y=
| 2 |
| 3 |
∴Q(1,-6).
设直线BQ:y=kx+b(k≠0).则把B、Q的坐标代入,得
|
解得
|
∴直线BQ的解析式是:y=2x-8,
∴E(0,-8);
(2)由(1)知,B(4,0),E(0,-8),则OE=8,OB=4.

①如图1,若∠COB=∠EOB=90°.
当△BOC∽△BOE时,
| BO |
| BO |
| OC |
| OE |
当△COB∽△BOE时,
| BO |
| EO |
| CO |
| BO |
| 4 |
| 8 |
| CO |
| 4 |
②如图1,若∠CBO=∠EOB=90°.
当△CBO∽△BOE时,
| CB |
| BO |
| BO |
| OE |
| CB |
| 4 |
| 4 |
| 8 |
当△OBC∽△BOE时,
| OB |
| BO |
| BC |
| OE |
③如图2,若∠OCB=∠BOE=90°,设C(x,y).
△OCB∽△BOE时,
| OC |
| BO |
| CB |
| OE |
| OC |
| 4 |
| CB |
| 8 |
| OC |
| CB |
| 1 |
| 2 |
∵直角△BOC中,根据勾股定理知OC2+BC2=OB2=16,②
∴由①②得,OC=
4
| ||
| 5 |
8
| ||
| 5 |
OC•BC=
| 32 |
| 5 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴y=
| 8 |
| 5 |
∴x=
| 4 |
| 5 |
| 4 |
| 5 |
| 8 |
| 5 |
同理,当△BCO∽△BOE时,C6(
| 16 |
| 5 |
| 8 |
| 5 |
综上所述,符合条件的点C的坐标是:
C1(0,8),C2(0,2),C3(4,2),C4(4,8),C5(
| 4 |
| 5 |
| 8 |
| 5 |
| 16 |
| 5 |
| 8 |
| 5 |
点评:本题考查了待定系数法求一次函数解析式,相似三角形的判定与性质以及二次函数的综合题.解答(2)题时,要分类讨论,以防漏解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013•闸北区一模)已知:如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点M、N分别在边AO和边OD上,且AM=
(2013•闸北区一模)已知:如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点M、N分别在边AO和边OD上,且AM= (2013•闸北区一模)已知:如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,EC和BD相交于点O,联接DE.
(2013•闸北区一模)已知:如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,EC和BD相交于点O,联接DE.