题目内容
【题目】如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC,垂足为E.若线段AE=2,则四边形ABCD的面积是_____.

【答案】4
【解析】
过点A作AF⊥AE,交CD的延长线于点F,由题意可证△ABE≌△ADF,可得AE=AF,则可证四边形AECF是正方形,四边形ABCD的面积=正方形AECF的面积=4.
解:过点A作AF⊥AE,交CD的延长线于点F
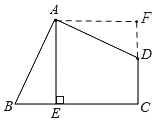
∵∠BAD=∠C=90°,AE⊥BC,AE⊥AF
∴四边形AECF是矩形
∴∠F=90°
∵AE⊥AF,BA⊥AD
∴∠BAE+∠DAE=90°,∠DAF+∠DAE=90°
∴∠BAE=∠DAF
又∵AB=AD,∠F=∠AEB=90°
∴△ADF≌△ABE
∴AF=AE,S△ADF=S△ABE.
∴四边形AECF是正方形.
∴S正方形AECF=![]() =4
=4
∵S四边形ABCD=S△ABE+S四边形AECD=S△ADF+S四边形AECD.
∴S四边形ABCD=S正方形AECF=4
故答案为:4

练习册系列答案
相关题目
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数.(如下表)
每人加工零件数 | 54 | 45 | 30 | 24 | 21 | 12 |
人 数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假设生产部负责人把每位工人的月加工零件数定为24件,你认为是否合理?为什么?如果不合理,请你设计一个较为合理的生产定额,并说明理由.




