جâؤ؟ؤعبف
،¾جâؤ؟،؟بçح¼1£¬شعئ½أوض±½ا×ّ±êدµضذ£¬A£¨a£¬0£©£¬B£¨0£¬2![]() £©
£©
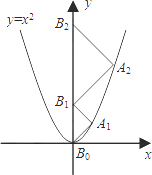
£¨1£©µم£¨k+1£¬2k©پ5£©¹طسعxضلµؤ¶ش³ئµمشعµعز»دَدق£¬aخھتµتkµؤ·¶خ§ؤعµؤ×î´َصûت£¬اَAµمµؤ×ّ±ê¼°،÷AOBµؤأو»£»
£¨2£©شع£¨1£©µؤجُ¼دآبçح¼1£¬µمPتاµعز»دَدقؤعµؤµم£¬از،÷ABPتازشABخھرüµؤµبرüض±½اب½اذخ£¬اëض±½سذ´³ِPµم×ّ±ê£»
£¨3£©شع£¨1£©µؤجُ¼دآ£¬بçح¼2£¬زشAB،¢OBµؤ×÷µب±ك،÷ABC؛حµب±ك،÷OBD£¬ء¬½سAD،¢OC½»سعEµم£¬ء¬½سBE£®
¢ظاَض¤£؛EBئ½·ض،دCED£»
¢عMµمتاyضلةدز»¶¯µم£¬اَAM+CM×îذ،ت±µمMµؤ×ّ±ê£®

،¾´ً°¸،؟£¨1£©A£¨2£¬0£©£¬S،÷AOB£½2![]() £»£¨2£©Pµم×ّ±êخھ£¨2+2
£»£¨2£©Pµم×ّ±êخھ£¨2+2![]() £¬2£©»ٍ£¨2
£¬2£©»ٍ£¨2![]() £¬2
£¬2![]() +2£©£»£¨3£©¢ظدê¼û½âخِ£»¢عM£¨0£¬
+2£©£»£¨3£©¢ظدê¼û½âخِ£»¢عM£¨0£¬![]() £©£®
£©£®
،¾½âخِ،؟
£¨1£©¸ù¾فµمشعµعثؤدَدقؤع£¬µأ³ِ²»µبت½£¬½ّ¶ّاَ³ِkµؤ·¶خ§£¬½ّ¶ّاَ³ِµمA×ّ±ê£¬×î؛َسأب½اذخأو»¹«ت½¼´؟ةµأ³ِ½لآغ£»
£¨2£©·ضء½ضضاé؟ِ£؛¹¹شىب«µبب½اذخاَ³ِPF؛حAF£¬¼´؟ةاَ³ِµمP×ّ±ê£»
£¨3£©¢ظدبإذ¶د³ِ،÷ABD،ص،÷CBO£¨SAS£©£¬½ّ¶ّµأ³ِS،÷ABD£½S،÷CBO£¬AD£½OC£¬¼´؟ةµأ³ِBM£½BN£¬×î؛َسأ½ائ½·ضدكµؤإذ¶¨¶¨ہي¼´؟ةµأ³ِ½لآغ£»
¢ع¸ù¾ف؛¬30¶ب½اµؤض±½اب½اذخµؤذشضتاَ³ِدك¶خµؤ³¤£¬½ّ¶ّاَ³ِµمC×ّ±ê£¬اَ³ِض±دكA'Cµؤ½âخِت½£¬¼´؟ةµأ³ِ½لآغ£®
½â£؛£¨1£©،كµم£¨k+1£¬2k©پ5£©¹طسعxضلµؤ¶ش³ئµمشعµعز»دَدق£¬
،àµم£¨k+1£¬2k©پ5£©شعµعثؤدَدق£¬
،àk+1£¾0£¬2k©پ5£¼0£¬
،à©پ1£¼k£¼2.5£¬
،كaخھتµتkµؤ·¶خ§ؤعµؤ×î´َصûت£¬
،àa£½2£¬
،كA£¨a£¬0£©£¬
،àA£¨2£¬0£©£¬
،àOA£½2£¬
،كB£¨0£¬2![]() £©£¬
£©£¬
،àOB£½2![]() £¬
£¬
،àS،÷AOB£½![]() OAOB£½
OAOB£½![]() ،ء
،ء![]() £½2
£½2![]() £»
£»
£¨2£©بçح¼1£¬
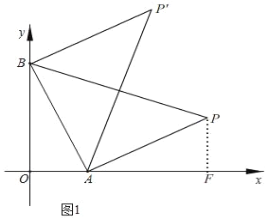
،كµمPتاµعز»دَدقؤعµؤµم£¬از،÷ABPتازشABخھرüµؤµبرüض±½اب½اذخ£¬
،à¢ظµ±،دBAP£½90،مت±£¬AB£½AP£¬
¹µمP×÷PF،حOAسعF£¬
،à،دPAF+،دAPF£½90،م£¬
،ك،دBAP£½90،م£¬
،à،دPAF+،دBAO£½90،م£¬
،à،دAPF£½،دBAO£¬
،كAB£½AP£¬
،à،÷OAB،ص،÷FPA£¨AAS£©£¬
،àPF£½OA£½2£¬AF£½OB£½2![]() £¬
£¬
،àOF£½OA+AF£½2+2![]() £¬
£¬
،àP£¨2+2![]() £¬2£©£¬
£¬2£©£¬
¢عµ±،دABP£½90،مت±£¬ح¬¢ظµؤ·½·¨µأ£¬P'£¨2![]() £¬2
£¬2![]() +2£©£¬
+2£©£¬
¼´£؛Pµم×ّ±êخھ£¨2+2![]() £¬2£©»ٍ£¨2
£¬2£©»ٍ£¨2![]() £¬2
£¬2![]() +2£©£»
+2£©£»
£¨3£©¢ظبçح¼2£¬
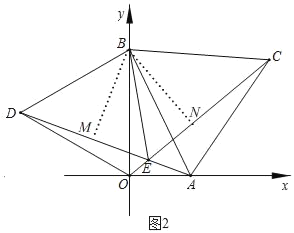
،ك،÷OBD؛ح،÷ABC¶¼تاµب±كب½اذخ£¬
،àBD£½OB£¬AB£½BC£¬،دOBD£½،دABC£½60،م£¬
،à،دABD£½،دCBO£¬
شع،÷ABD؛ح،÷CBOضذ£¬ £¬
£¬
،à،÷ABD،ص،÷CBO£¨SAS£©£¬
،àS،÷ABD£½S،÷CBO£¬AD£½OC£¬
¹µمB×÷BM،حADسعM£¬BN،حOCسعN£¬
،àBM£½BN£¬
،كBM،حAD£¬BN،حOC£¬
،àBEتا،دCEDµؤ½ائ½·ضدك£»
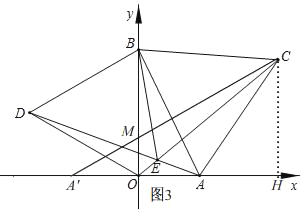
¢عبçح¼3£¬
×÷µمA¹طسعyضلµؤ¶ش³ئµمA'£¬
،كA£¨2£¬0£©£¬
،àA'£¨©پ2£¬0£©£¬
ء¬½سA'C½»yضلسعM£¬
¹µمC×÷CH،حOAسعH£¬
شعRt،÷AOBضذ£¬OA£½2£¬OB£½2![]() £¬
£¬
،àAB£½4£¬tan،دOAB£½![]() £½
£½![]() £½
£½![]() £¬
£¬
،à،دOAB£½60،م£¬
،ك،÷ABCتاµب±كب½اذخ£¬
،àAC£½AB£½4£¬،دBAC£½60،م£¬
،à،دCAH£½60،م£¬
شعRt،÷ACHضذ£¬،دACH£½90،م©پ،دCAH£½30،م£¬
،àAH£½2£¬CH£½2![]() £¬
£¬
،àOH£½OA+AH£½4£¬
،àµمC£¨4£¬2![]() £©£¬
£©£¬
،كA'£¨©پ2£¬0£©£¬
،àض±دكA'Cµؤ½âخِت½خھy£½![]() x+
x+![]() £¬
£¬
،àM£¨0£¬![]() £©£®
£©£®

 خؤ¾´ح¼تé؟خت±دب·ودµءذ´ً°¸
خؤ¾´ح¼تé؟خت±دب·ودµءذ´ً°¸