题目内容
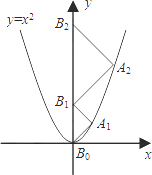
【题目】如图,正比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于点
的图像交于点![]() ,一次函数的图像经过点
,一次函数的图像经过点![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() .
.

(1)求一次函数的表达式;
(2)二元一次方程组![]() 的解为________________;
的解为________________;
(3)当![]() 与
与![]() 同时成立时,
同时成立时,![]() 的取值范围为__________;
的取值范围为__________;
(4)求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)4
;(4)4
【解析】
(1)正比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于点
的图像交于点![]() ,已知正比例函数解析式可求得a,又因为一次函数的图像经过点
,已知正比例函数解析式可求得a,又因为一次函数的图像经过点![]() ,即可求出一次函数解析式.
,即可求出一次函数解析式.
(2)把两个一次函数解析式合成一个二元一次方程组,这个方程组的解就是它们的交点坐标.即可求解.
(3)分别求出![]() 与
与![]() 时x的取值范围,再取交集,即可求解.
时x的取值范围,再取交集,即可求解.
(4)(1)中已求得A点坐标,再求得OD长即可求出![]() 的面积.
的面积.
∵正比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于点
的图像交于点![]()
![]()
∴![]()
又∵一次函数的图像经过点![]()
∴![]()
∴![]()
∴一次函数的表达式为:![]()
故答案为:![]()
(2)二元一次方程组![]() 的解即为正比例函数
的解即为正比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交点坐标
的图像交点坐标
∵正比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于点
的图像交于点![]()
∴二元一次方程组![]() 的解为:
的解为:![]()
故答案为:![]()
(3)当![]() 时
时
可得![]()
当![]() 时
时
∴![]()
∴![]()
∴当![]() 与
与![]() 同时成立时,
同时成立时,![]() 的取值范围为
的取值范围为![]()
故答案为:![]()
(3)令![]()
∴![]()
即OD=2
又∵![]()
S△AOD=![]() =4
=4
故答案为:4

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数.(如下表)
每人加工零件数 | 54 | 45 | 30 | 24 | 21 | 12 |
人 数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假设生产部负责人把每位工人的月加工零件数定为24件,你认为是否合理?为什么?如果不合理,请你设计一个较为合理的生产定额,并说明理由.