题目内容
【题目】已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BP作垂线,垂足分别为E、F,点O为AC的中点.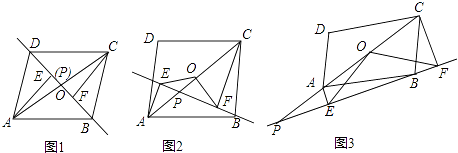
(1)当点P与点O重合时如图1,求证:OE=OF
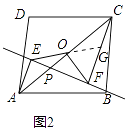
(2)直线BP绕点B逆时针方向旋转,当点P在对角线AC上时,且∠OFE=30°时,如图2,猜想线段CF、AE、OE之间有怎样的数量关系?并给予证明.
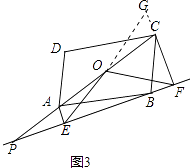
(3)当点P在对角线CA的延长线上时,且∠OFE=30°时,如图3,猜想线段CF、AE、OE之间有怎样的数量关系?直接写出结论即可.
【答案】
(1)
解:∵AE⊥PB,CF⊥BP,
∴∠AEO=∠CFO=90°,
在△AEO和△CFO中,
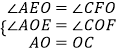 ,
,
∴△AOE≌△COF(AAS),
∴OE=OF
(2)
解:图2中的结论为:CF=OE+AE
选图2中的结论证明如下:
延长EO交CF于点G,
∵AE⊥BP,CF⊥BP,
∴AE∥CF,
∴∠EAO=∠GCO,
在△EOA和△GOC中,
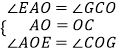 ,
,
∴△EOA≌△GOC(ASA),
∴EO=GO,AE=CG,
在Rt△EFG中,∵EO=OG,
∴OE=OF=GO,
∵∠OFE=30°,
∴∠OFG=90°﹣30°=60°,
∴△OFG是等边三角形,
∴OF=GF,
∵OE=OF,
∴OE=FG,
∵CF=FG+CG,
∴CF=OE+AE
(3)
解:图3中的结论为:CF=OE﹣AE
选图3的结论证明如下:
延长EO交FC的延长线于点G,
∵AE⊥BP,CF⊥BP,
∴AE∥CF,
∴∠AEO=∠G,
在△AOE和△COG中,
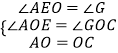 ,
,
∴△AOE≌△COG(AAS),
∴OE=OG,AE=CG,
在Rt△EFG中,∵OE=OG,
∴OE=OF=OG,
∵∠OFE=30°,
∴∠OFG=90°﹣30°=60°,
∴△OFG是等边三角形,
∴OF=FG,
∵OE=OF,
∴OE=FG,
∵CF=FG﹣CG,
∴CF=OE﹣AE.
【解析】(1)由△AOE≌△COF即可得出结论.(2)图2中的结论为:CF=OE+AE,延长EO交CF于点G,只要证明△EOA≌△GOC,△OFG是等边三角形,即可解决问题.(3)图3中的结论为:CF=OE﹣AE,延长EO交FC的延长线于点G,证明方法类似.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°.

【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.