题目内容
【题目】课本中有一个例题： 有一个窗户形状如图1，上部是一个半圆，下部是一个矩形，如果制作窗框的材料总长为6m，如何设计这个窗户，使透光面积最大？
这个例题的答案是：当窗户半圆的半径约为0.35m时，透光面积最大值约为1.05m2 ．
我们如果改变这个窗户的形状，上部改为由两个正方形组成的矩形，如图2，材料总长仍为6m，利用图3，解答下列问题：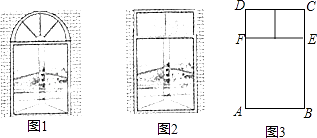
（1）若AB为1m，求此时窗户的透光面积？
（2）与课本中的例题比较，改变窗户形状后，窗户透光面积的最大值有没有变大？请通过计算说明．
【答案】
（1）解：由已知可得：AD= 
，
则S=1× 
m2
（2）解：设AB=xm，则AD=3﹣ 
m，
∵ 
，
∴ 
，
设窗户面积为S，由已知得：
，
当x= 
m时，且x= m在 的范围内， 
，
∴与课本中的例题比较，现在窗户透光面积的最大值变大
【解析】（1）根据矩形和正方形的周长进行解答即可；（2）设AB为xcm，利用二次函数的最值解答即可．
春雨教育同步作文系列答案
【题目】自行车厂某周计划生产2100辆电动车，平均每天生产电动车300辆．由于各种原因，实际每天的生产量与计划每天的生产量相比有出入，下表是该周的实际生产情况（超产记为正、减产记为负，单位：辆）：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
减增 |
|
|
|
|
|
|
|
（1）该厂星期一生产电动车________辆；
(2)生产量最多的一天比生产量最少的一天多生产电动车________辆；
(3)该厂实行记件工资制，每生产一辆车可得60元，那么该厂工人这一周的工资总额是多少元？
【题目】观察下列一组勾股数：
|
|
| |
第1组 | 3=2×1+1 | 4=2×1×（1+1） | 5=2×1×（1+1）+1 |
第2组 | 5=2×2+1 | 12=2×2×（2+1） | 13=2×2×（2+1）+1 |
第3组 | 7=2×3+1 | 24=2×3×（3+1） | 25=2×3×（3+1）+1 |
第4组 | 9=2×4+1 | 40=2×4×（4+1） | 41=2×4×（4+1）+1 |
… | … | … | … |
观察以上各组勾股数的特点：
（1）请写出第7组勾股数
，
，
；
（2）写出第
组勾股数，
.
