题目内容
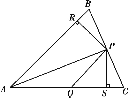
【题目】如图,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,∠CAP=∠APQ,PR=PS,下面的结论:①AS=AR;②QP∥AR;③△BRP≌△CSP.其中正确的是( )
A. ①② B. ②③ C. ①③ D. ①②③
【答案】A
【解析】
连接AP,由已知条件利用角平行线的判定可得∠1=∠2,由三角形全等的判定得△APR≌△APS,得AS=AR,由已知可得∠2=∠3,得到∠1=∠3,得QP∥AR,答案可得.
连接AP,
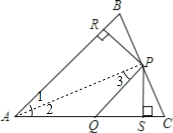
∵PR=PS,PR⊥AB,垂足为R,PS⊥AC,垂足为S,
∴AP是∠BAC的平分线,∠1=∠2,
∴△APR≌△APS,
∴AS=AR,
又AQ=PQ,
∴∠2=∠3,
又∠1=∠2,
∴∠1=∠3,
∴QP∥AR,
BC只是过点P,没有办法证明△BRP≌△CSP,③不成立.
故选A.

练习册系列答案
相关题目
【题目】某学校抽查了某班级某月10天的用电量,数据如下表:
用电量/度 | 8 | 9 | 10 | 13 | 14 | 15 |
天数 | 1 | 1 | 2 | 3 | 1 | 2 |
(1)这10天用电量的众数是______度,中位数是______度;
(2)求这个班级平均每天的用电量;
(3)该校共有20个班级,该月共计30天,试估计该校该月总的用电量.