题目内容
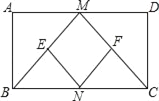
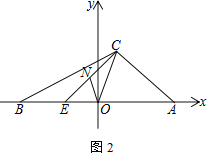
【题目】如图,菱形![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 交对角线
交对角线![]() 于点
于点![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
(1)请你根据题意补全图形;
(2)若![]() ,则菱形
,则菱形![]() 的面积为 .(直接写出答案)
的面积为 .(直接写出答案)
(3)请用等式表示线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
【答案】(1)画图见解析;(2)50![]() ;(3)
;(3)![]() ,证明见解析.
,证明见解析.
【解析】
(1)根据已知条件画图即可;(2)根据菱形的面积计算公式计算即可.
(3)取AE中点G,连接GF、GD,证明△DGF是直角三角形,在Rt△DGF中,利用GD2+GF2=DF2,可推导出DF、AE、BC之间的数量关系.
(1)如图1: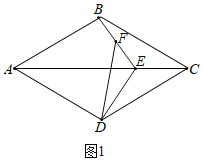
(2)50![]() .理由如下:
.理由如下:
设菱形AD边上的高为h,则h=ABsin60°=10×![]() =5
=5![]() .
.
∴菱形![]() 的面积=10×5
的面积=10×5![]() =50
=50![]() .
.
(3)DF、BC、AE之间的数量关系是:AE2+BC2=4DF2.
证明:取AE中点G,连接GF、GD.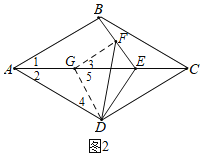
∵四边形ABCD是菱形,∠BAD=60°,
∴∠1=∠2=![]() ∠BAD=30°,AB=BC.
∠BAD=30°,AB=BC.
∵点F是BE的中点,
∴GF是△ABE的中位线.
∴GF=![]() AB,GF∥AB.
AB,GF∥AB.
∴∠3=∠1=30°.
∵ED⊥AD于D,
∴在Rt△ADE中,DG=AG=![]() AE.
AE.
∴∠2=∠4=30°.
∴∠5=60°.
∴∠FGD=∠3+∠5=90°.
∴在Rt△DGF中,GD2+GF2=DF2.
∴(![]() AE)2+(
AE)2+(![]() BC)2=DF2.
BC)2=DF2.
即AE2+BC2=4DF2.

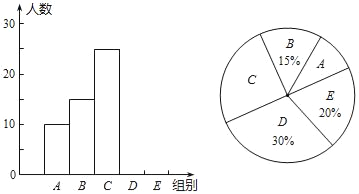
【题目】我校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确数字x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)有三位评委老师,每位老师在E组学生完成学校比赛后,出示“通过”或“淘汰”或“待定”的评定结果.学校规定:每位学生至少获得两位评委老师的“通过”才能代表学校参加鄂州市“汉字听写”比赛,请用树形图求出E组学生王云参加鄂州市“汉字听写”比赛的概率.