题目内容
【题目】已知![]() 中,
中,![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() 为
为![]() 上一点,
上一点,![]() ,设
,设![]() ,
,![]()
(1)若![]() ,
,![]() ,则
,则![]() __________;
__________;![]() __________;若
__________;若![]() ,
,![]() ,则
,则![]() __________;
__________;![]() __________;
__________;
(2)由此猜想![]() 与
与![]() 的关系,并证明.
的关系,并证明.
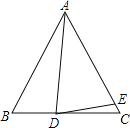
【答案】(1)见解析;(2)![]()
【解析】
(1)先利用等腰三角形的性质求出∠DAE,进而求出∠BAD,即可得出结论;
(2)利用等腰三角形的性质和三角形的内角和即可得出结论.
解:(1)①∵AB=AC,∠ABC=60°,
∴∠BAC=60°,
∵AD=AE,∠ADE=70°,
∴∠DAE=180°-2∠ADE=40°,
∴α=∠BAD=60°-40°=20°,
∴∠ADC=∠BAD+∠ABD=60°+20°=80°,
∴β=∠CDE=∠ADC-∠ADE=10°,
②同理α=30°;β=15°.
故答案为:20°,10°,30°,15°;
(2)猜想α=2β,理由如下:
设∠ABC=x,∠AED=y,
∴∠ACB=x,∠ADE=y
在△DEC中,y=β+x,
在△ABD中,α+x=y+β=β+x+β,
∴α=2β.

练习册系列答案
相关题目
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对
他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:s2=![]() [
[![]() ])
])