题目内容
【题目】如图,△ABC是半径为2的⊙O的内接三角形,连接OA、OB,点D、E、F、G分别是CA、OA、OB、CB的中点. 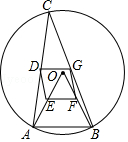
(1)试判断四边形DEFG的形状,并说明理由;
(2)填空: ①若AB=3,当CA=CB时,四边形DEFG的面积是;
②若AB=2,当∠CAB的度数为时,四边形DEFG是正方形.
【答案】
(1)解:四边形DEFG是平行四边形.
∵点D、E、F、G分别是CA、OA、OB、CB的中点,
∴DG∥AB,DG= ![]() AB,EF∥AB,EF=
AB,EF∥AB,EF= ![]() AB,
AB,
∴DG∥EF,DG=EF,
∴四边形DEFG是平行四边形;
(2)![]() ;75°或15°
;75°或15°
【解析】解:(2)①连接OC. 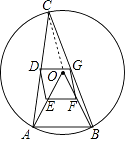
∵CA=CB,
∴ ![]() =
= ![]() ,
,
∴DG⊥OC,
∵AD=DC,AE=EO,
∴DE∥OC,DE= ![]() OC=1,同理EF=
OC=1,同理EF= ![]() AB=
AB= ![]() ,
,
∴DE⊥DG,
∴四边形DEFG是矩形,
∴四边形DEFG的面积= ![]() .
.
所以答案是 ![]() ;②当C是优弧AB的中点时,四边形DEFG是正方形,此时∠CAB=75°,
;②当C是优弧AB的中点时,四边形DEFG是正方形,此时∠CAB=75°,
当C是劣弧AB的中点时,四边形DEFG是正方形,此时∠CAB=15°,
所以答案是75°或15°.
【考点精析】认真审题,首先需要了解正方形的判定方法(先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角),还要掌握三角形的外接圆与外心(过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心)的相关知识才是答题的关键.

练习册系列答案
相关题目