Question

【题目】如图，以x=1为对称轴的抛物线y=ax2+bx+c的图象与x轴交于点A，点B（﹣1，0），与y轴交于点C（0，4），作直线AC．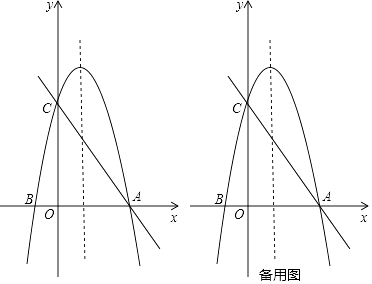

（1）求抛物线解析式；
（2）点P在抛物线的对称轴上，且到直线AC和x轴的距离相等，设点P的纵坐标为m，求m的值；
（3）点M在y轴上且位于点C上方，点N在直线AC上，点Q为第一象限内抛物线上一点，若以点C、M、N、Q为顶点的四边形是菱形，请直接写出点Q的坐标．

Answer 1

【答案】
（1）

解：∵点A与点B（﹣1，0）关于直线x=1对称，

∴A（3，0），

设抛物线解析式为y=a（x+1）（x﹣3），

把C（0，4）代入得a1（﹣3）=4，解得a=﹣ ，

∴抛物线解析式为y=﹣ （x+1）（x﹣3），即y=﹣ x2+ x+4；

（2）

解：设直线AC的解析式为y=kx+p，

把A（3，0），C（0，4）代入得 ，解得 ，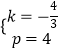

∴直线AC的解析式为y=﹣ x+4；

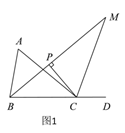
令对称轴与直线AC交于点D，与x轴交于点E，作PH⊥AD于H，如图1，

当x=1时，y=﹣ x+4= ，则D（1， ），

∴DE= ，

在Rt△ADE中，AD= = ，

设P（1，m），则PD= ﹣m，PH=PE=|m|，

∵∠PDH=∠ADE，

∴△DPH∽△DAE，

∴ = ，即 = ，解得m=1或m=﹣4，

即m的值为1或﹣4；

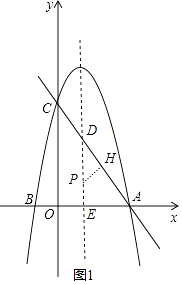
（3）

解：设Q（t，﹣ t2+ t+4）（0＜t＜4），

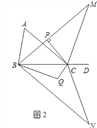
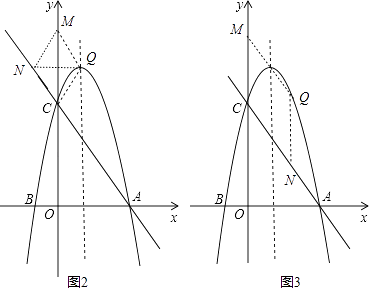
当CM为对角线时，四边形CQMN为菱形，如图2，则点N和Q关于y轴对称，

∴N（﹣t，﹣ t2+ t+4），

把N（﹣t，﹣ t2+ /span> t+4）代入y=﹣ x+4得 t+4=﹣ t2+ t+4，解得t1=0（舍去），t2=1，此时Q点坐标为（1， ）；

当CM为菱形的边时，四边形CNQM为菱形，如图3，则NQ∥y轴，NQ=NC，

∴N（t，﹣ t+4），

∴NQ=﹣ t2+ t+4﹣（﹣ t+4）=﹣ t2+4t，

而CN2=t2+（﹣ t+4﹣4）2= t2，即CN= t，

∴﹣ t2+4t= t，解得t1=0（舍去），t2= ，此时Q点坐标为（ ， ），

综上所述，点Q的坐标为（1， ）或（ ， ）．

【解析】（1）先利用抛物线的对称性得到A（3，0），则可设交点式y=a（x+1）（x﹣3），然后把C点坐标代入求出a即可；（2）先利用待定系数法其出直线AC的解析式为y=﹣ x+4；令对称轴与直线AC交于点D，与x轴交于点E，作PH⊥AD于H，如图1，易得D（1， ），利用勾股定理计算出AD= ，设P（1，m），则PD= ﹣m，PH=PE=|m|，证明△DPH∽△DAE，利用相似比得到 = ，然后解方程可得到m的值；（3）设Q（t，﹣ t2+ t+4）（0＜t＜4），讨论：当CM为对角线时，四边形CQMN为菱形，如图2，根据菱形的性质判定点N和Q关于y轴对称，则N（﹣t，﹣ t2+ t+4），然后
把N（﹣t，﹣ t2+ t+4）代入y=﹣ x+4得t的方程，从而解方程求出t得到此时Q点坐标；当CM为菱形的边时，四边形CNQM为菱形，如图3，利用菱形的性质得NQ∥y轴，NQ=NC，则N（t，﹣ t+4），所以NQ=﹣ t2+4t，再根据两点间的距离公式计算出CN= t，所以﹣ t2+4t= t，从而解方程求出t得到此时Q点坐标．
【考点精析】本题主要考查了二次函数的性质的相关知识点，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．