Question

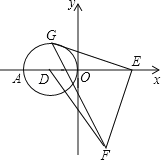
【题目】如图，平面直角坐标系中，点A（﹣4，0），点E （4，0），以AO为直径作⊙D，点G是⊙D上一动点，以EG为腰向下作等腰直角三角形EGF，连接DF，则DF的最大值是_____．

Answer 1

【答案】6+2

【解析】

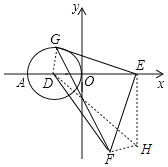
如图，连接DG，过点E作EH⊥AE，且DE＝EH，连接DH，FH，由“SAS”可证△GDE≌△HFE，可得GD＝FH＝2，可得点F在以H为圆心，2为半径的圆上，即可求DF的最大值．

如图，连接DG，过点E作EH⊥AE，且DE＝EH，连接DH，FH，

∵点A（﹣4，0），点E （4，0），

∴AO＝4＝OE，

∵AO是圆D直径，

∴，

∴DE＝6＝EH，且EH⊥AE，

∴DH＝6，

∵EGF是等腰直角三角形，

∴GE＝EF，∠GEF＝∠DEH＝90°，

∴∠GED＝∠FEH，且GE＝EF，DE＝EH，

∴△GDE≌△HFE（SAS）

∴GD＝FH＝2，

∴点F在以H为圆心，2为半径的圆上，

∴当点F在DH的延长线上时，DF有最大值，

∴DF的最大值为6+2，

故答案为：6+2．