题目内容
【题目】创客联盟的队员想用3D的打印完成一幅边长为6米的正方形作品ABCD,设计图案如图所示(四周阴影是四个全等的矩形,用材料甲打印;中心区是正方形MNPQ,用材料乙打印).在打印厚度保持相同的情况下,两种材料的消耗成本如表:
材料 | 甲 | 乙 |
价格(元/米2) | 50 | 40 |
设矩形的较短边AH的长为x米,打印材料的总费用为y元.
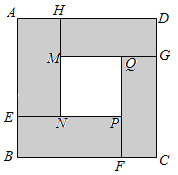
(1)MQ的长为 米(用含x的代数式表示);
(2)求y关于x的函数解析式;
(3)当中心区的边长不小于2米时,预备资金1700元购买材料一定够用吗?请说明理由.
【答案】(1)(6﹣2x);(2)y=﹣40x2+240x+1440;(3)预备资金1700元购买材料一定够用.理由见解析
【解析】
(1)根据大正方形的边长减去两个小长方形的宽即可求解;
(2)根据总费用等于两种材料的费用之和即可求解;
(3)根据(2)中求得的关系式代入求解,解出x的值后再根据二次函数的性质解答.
解:(1)根据题意,得:MQ=AD﹣2AH=6﹣2x.
故答案为(6﹣2x);
(2)根据题意,得AH=x,AE=6﹣x,
S甲=4S长方形AENH=4x(6﹣x)=24x﹣4x2,S乙=S正方形MNQP=(6﹣2x)2=36﹣24x+4x2.
∴y=50(24x﹣4x2)+40(36﹣24x+4x2)=﹣40x2+240x+1440;
答:y关于x的函数解析式为y=﹣40x2+240x+1440.
(3)预备资金1700元购买材料一定够用.理由如下:
当y=1700时,1700=﹣40x2+240x+1440,解得x1=![]() ,x2=
,x2=![]() .
.
∵中心区的边长不小于2米,即6﹣2x≥2,解得x≤2,∴0<x≤2,∴x=![]() .
.
∵y=﹣40x2+240x+1440=﹣40(x-3)2+1800,![]() ,对称轴是直线x=3,
,对称轴是直线x=3,
∴当0<x≤2时,y随x的增大而增大,
∴当![]() 时,
时,![]() .
.
∴预备资金1700元购买材料一定够用.