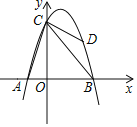题目内容
【题目】某货车销售公司,分别试销售两种型号货车各一个月,并从中选择一种长期销售,设每月销售量为x辆若销售甲型货车,每月销售的利润为y1(万元),已知每辆甲型货车的利润为(m+6)万元,(m是常数,9≤m≤11),每月还需支出其他费用8万元,受条件限制每月最多能销售甲型货车25辆;若销售乙型货车,每月的利润y2(万元)与x的函数关系式为y2=ax2+bx-25,且当x=10时,y2=20,当x=20时,y2=55,受条件限制每月最多能销售乙型货车40辆.
(1)分别求出y1、y2与x的函数关系式,并确定x的取值范范围;
(2)分别求出销售这两种货车的最大月利润;(最大利润能求值的求值,不能求值的用式子表示)
(3)为获得最大月利润,该公司应该选择销售哪种货车?请说明理由.
【答案】(1)y1=(m+6)x﹣8(0≤x≤25);y2=﹣![]() x2+5x﹣25(0≤x≤40);(2)当x=25时,y1 取得最大值,最大值为25m+142.当x=40时,y2有最大值,最大值为95.(3)应选择甲种货车,理由见解析.
x2+5x﹣25(0≤x≤40);(2)当x=25时,y1 取得最大值,最大值为25m+142.当x=40时,y2有最大值,最大值为95.(3)应选择甲种货车,理由见解析.
【解析】
(1)根据待定系数法即可求出两个函数解析式;(2)根据函数的性质和自变量的取值范围即可求解;(3)根据函数的最大值即可求得结果.
解:(1)根据题意,得
y1=(m+6)x﹣8,(0≤x≤25).
将x=10、y2=20,x=20、y2=55代入y2=ax2+bx﹣25,![]()
解得: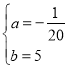
∴y2=![]() ,(0≤x≤40).
,(0≤x≤40).
(2)∵m是常数,(9≤m≤11),∴m+6>0,
∴y1 随x的增大而增大,
∴当x=25时,y1 取得最大值,最大值为25m+142.
∵y2=﹣![]() (x﹣50)2+100,
(x﹣50)2+100,
∴当x<50时,y随x的增大而增大,
∵0≤x≤40,
∴当x=40时,y2有最大值,最大值为95.
(3)∵y1 的最大值为25m+142.且9≤m≤11,
∴367≤y1≤417,
y2 有最大值为95,
∴95<367.
故应选择甲种货车.

 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案【题目】某食品厂生产一种半成品食材,成本为2元/千克,每天的产量![]() (百千克)与销售价格
(百千克)与销售价格![]() (元/千克)满足函数关系式
(元/千克)满足函数关系式![]() ,从市场反馈的信息发现,该半成品食材每天的市场需求量
,从市场反馈的信息发现,该半成品食材每天的市场需求量![]() (百千克)与销售价格
(百千克)与销售价格![]() (元/千克)满足一次函数关系,部分数据如表:
(元/千克)满足一次函数关系,部分数据如表:
销售价格 | 2 | 4 | …… | 10 |
市场需求量 | 12 | 10 | …… | 4 |
已知按物价部门规定销售价格![]() 不低于2元/千克且不高于10元/千克.
不低于2元/千克且不高于10元/千克.
(1)直接写出![]() 与
与![]() 的函数关系式,并注明自变量
的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
(2)当每天的产量小于或等于市场需求量时,这种半成品食材能全部售出,而当每天的产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃.
①当每天的半成品食材能全部售出时,求![]() 的取值范围;
的取值范围;
②求厂家每天获得的利润y(百元)与销售价格![]() 的函数关系式;
的函数关系式;
(3)在(2)的条件下,当![]() 为______元/千克时,利润
为______元/千克时,利润![]() 有最大值;若要使每天的利润不低于24(百元),并尽可能地减少半成品食材的浪费,则
有最大值;若要使每天的利润不低于24(百元),并尽可能地减少半成品食材的浪费,则![]() 应定为______元/千克.
应定为______元/千克.