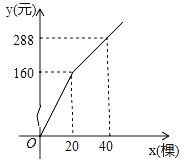
题目内容
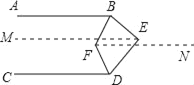
【题目】如图,AB∥CD , ∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD= ( )
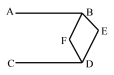
A.110°B.115°C.125°D.130°
【答案】C
【解析】
先过点E作EM∥AB,过点F作FN∥AB,由AB∥CD,即可得EM∥AB∥CD∥FN,然后根据两直线平行,同旁内角互补,由∠BED=110°,即可求得∠ABE+∠CDE=250°,又由BF平分∠ABE,DF平分∠CDE,根据角平分线的性质,即可求得∠ABF+∠CDF的度数,又由两直线平行,内错角相等,即可求得∠BFD的度数.
解:如图,过点E作EM∥AB,过点F作FN∥AB,
∵AB∥CD,
∴EM∥AB∥CD∥FN,
∴∠ABE+∠BEM=180°,∠CDE+∠DEM=180°,
∴∠ABE+∠BED+∠CDE=360°,
∵∠BED=110°,
∴∠ABE+∠CDE=250°
∵BF平分∠ABE,DF平分∠CDE,
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠ABF+∠CDF=![]() (∠ABE+∠CDE)=125°,
(∠ABE+∠CDE)=125°,
∵∠DFN=∠CDF,∠BFN=∠ABF,
∴∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=125°.
故选:C.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目