��Ŀ����
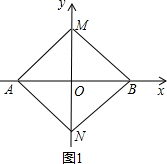
��ͼ����ƽ��ֱ������ϵ�У���֪�ı���ABCD�ǵ������Σ�A��B��x���ϣ�D��y��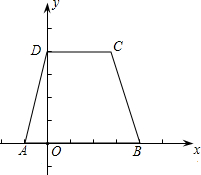 �ϣ�AB��CD��AD=BC=
�ϣ�AB��CD��AD=BC=
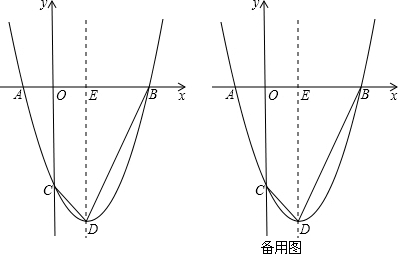
��AB=5��CD=3��������y=-x2+bx+c��A��B���㣮
��1����b��c��
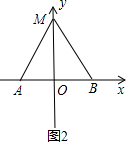
��2����M��x���Ϸ��������ϵ�һ���㣬����x����y��ľ���֮��Ϊd����d�����ֵ��
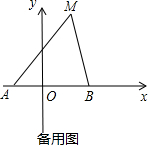
��3������2����M���˶���ʹdȡ���ֵʱ����ʱ�ǵ�MΪN�����߶�AC��y�ύ�ڵ�E��FΪ�߶�EC��һ���㣬��F��N���뵽y��ľ���֮�͵���Сֵ�������ʱF������꣮
 �ϣ�AB��CD��AD=BC=
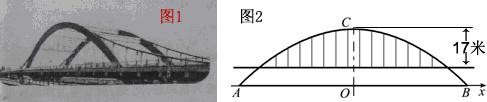
�ϣ�AB��CD��AD=BC=| 17 |
��1����b��c��
��2����M��x���Ϸ��������ϵ�һ���㣬����x����y��ľ���֮��Ϊd����d�����ֵ��
��3������2����M���˶���ʹdȡ���ֵʱ����ʱ�ǵ�MΪN�����߶�AC��y�ύ�ڵ�E��FΪ�߶�EC��һ���㣬��F��N���뵽y��ľ���֮�͵���Сֵ�������ʱF������꣮
��1����A��-1��0��B��4��0����
��x=-1��y=0��
x=4��y=0�ֱ����y=-x2+bx+c��
��
��
���
����3�֣�
��2����M��������a��-a2+3a+4����
d=|a|-a2+3a+4��
�ٵ�-1��a��0ʱ��d=-a2+2a+4=-��a-1��2+5��
���ԣ���a=0ʱ��dȡ���ֵ��ֵΪ4��
�ڵ�0��a��4ʱ��d=-a2+4a+4=-��a-2��2+8
���ԣ���a=2ʱ��dȡ���ֵ�����ֵΪ8��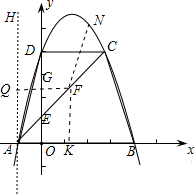
�ۺϢ١��ڵã�d�����ֵΪ8��
��������a��ȡֵ����ó���ȷ����ĵ�2�֣�
��3��N���������2��6����
��A��y���ƽ����AH����F��FG��y�ύAH�ڵ�Q����F��FK��x����K��
�ߡ�CAB=45�㣬ACƽ�֡�HAB��
��FQ=FK
��FN+FG=FN+FK-1��
���ԣ���N��F��K��һ��ֱ����ʱ��FN+FG=FN+FK-1��С����СֵΪ5��
����ֱ��AC�ĺ�����ϵʽΪy=x+1����x=2����y=x+1��y=3��
����F���������2��3����
��x=-1��y=0��
x=4��y=0�ֱ����y=-x2+bx+c��
��
|
���
|
��2����M��������a��-a2+3a+4����
d=|a|-a2+3a+4��
�ٵ�-1��a��0ʱ��d=-a2+2a+4=-��a-1��2+5��
���ԣ���a=0ʱ��dȡ���ֵ��ֵΪ4��
�ڵ�0��a��4ʱ��d=-a2+4a+4=-��a-2��2+8
���ԣ���a=2ʱ��dȡ���ֵ�����ֵΪ8��
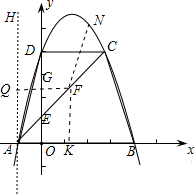
�ۺϢ١��ڵã�d�����ֵΪ8��
��������a��ȡֵ����ó���ȷ����ĵ�2�֣�
��3��N���������2��6����
��A��y���ƽ����AH����F��FG��y�ύAH�ڵ�Q����F��FK��x����K��
�ߡ�CAB=45�㣬ACƽ�֡�HAB��
��FQ=FK
��FN+FG=FN+FK-1��
���ԣ���N��F��K��һ��ֱ����ʱ��FN+FG=FN+FK-1��С����СֵΪ5��
����ֱ��AC�ĺ�����ϵʽΪy=x+1����x=2����y=x+1��y=3��
����F���������2��3����

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ