题目内容
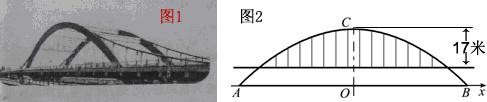
徒骇河大桥是我市第一座特大型桥梁,大桥桥体造型新颖,气势恢宏,两条拱肋如长虹卧波,极具时代气息(如图①).大桥为中承式悬索拱桥,大桥的主拱肋ACB是抛物线的一部分(如图②),跨径AB为100m,拱高OC为25m,抛物线顶点C到桥面的距离为17m.
(1)请建立适当的坐标系,求该抛物线所对应的函数关系式;
(2)七月份汛期来临,河水水位上涨,假设水位比AB所在直线高出1.96m,这时位于水面上的拱肋的跨径是多少?在不计桥面厚度的情况,一条高出水面4.6m的游船是否能够顺利通过大桥?
(1)请建立适当的坐标系,求该抛物线所对应的函数关系式;
(2)七月份汛期来临,河水水位上涨,假设水位比AB所在直线高出1.96m,这时位于水面上的拱肋的跨径是多少?在不计桥面厚度的情况,一条高出水面4.6m的游船是否能够顺利通过大桥?

(1)以AB所在直线为x轴,直线OC为y轴,建立直角坐标系,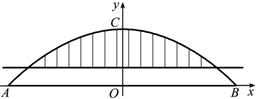
如图所示:设抛物线所对应的函数关系式为y=ax2+c,由题意得B(50,0),C(0,25)
∴
解得a=-
,c=25
∴抛物线对应的函数关系式是y=-
x2+25;
(2)当水位比AB所在直线高出1.96米时,
将y=1.96代入函数关系式得1.96=-
x2+25,
得x=±48,
∴由题意:48×2=96米,
故位于水面上的拱肋的跨径是96米,
根据题意,游船的最高点到桥面的距离为(25-17)-(1.96+4.6)=1.44米,
所以游船能顺利通过大桥.

如图所示:设抛物线所对应的函数关系式为y=ax2+c,由题意得B(50,0),C(0,25)
∴
|
解得a=-
| 1 |
| 100 |
∴抛物线对应的函数关系式是y=-
| 1 |
| 100 |
(2)当水位比AB所在直线高出1.96米时,
将y=1.96代入函数关系式得1.96=-
| 1 |
| 100 |
得x=±48,
∴由题意:48×2=96米,
故位于水面上的拱肋的跨径是96米,
根据题意,游船的最高点到桥面的距离为(25-17)-(1.96+4.6)=1.44米,
所以游船能顺利通过大桥.

练习册系列答案
相关题目
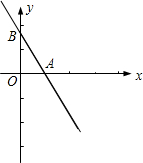 于点B,tan∠OAB=
于点B,tan∠OAB= 60°.飞机继续飞行0.1千米到达E处进行空投,已知空投物资在空中下落过程中的轨迹是抛物线,若要使空投物资刚好落在O处.
60°.飞机继续飞行0.1千米到达E处进行空投,已知空投物资在空中下落过程中的轨迹是抛物线,若要使空投物资刚好落在O处.

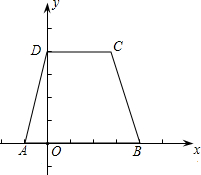 上,AB
上,AB