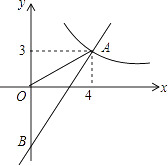题目内容
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),点P是x轴上一动点,过点P作x轴的垂线交抛物线于点C,交直线AB于点D,设P(x,0).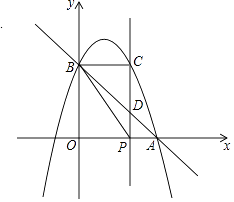
(1)求抛物线的函数表达式;
(2)当0<x<3时,求线段CD的最大值;
(3)在△PDB和△CDB中,当其中一个三角形的面积是另一个三角形面积的2倍时,求相应x的值;
(4)过点B,C,P的外接圆恰好经过点A时,x的值为 . (直接写出答案)
【答案】
(1)解:∵抛物线y=﹣x2+bx+c与x轴正半轴交于点A(3,0),与y轴交于点B(0,3),
∴﹣9+3b+c=0,c=3,
∴b=2,
∴抛物线解析式为y=﹣x2+2x+3;
(2)解:∵A(3,0),B(0,3),∴直线AB解析式为y=﹣x+3,
∵P(x,0).
∴D(x,﹣x+3),C(x,﹣x2+2x+3),
∵0<x<3,
∴CD=﹣x2+2x+3﹣(﹣x+3)=﹣x2+3x=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
当x= ![]() 时,CD最大=
时,CD最大= ![]() ;
;
(3)解:由(2)知,CD=|﹣x2+3x|,DP=|﹣x+3|
①当S△PDB=2S△CDB时,
∴PD=2CD,
即:2|﹣x2+3x|=|﹣x+3|,
∴x=± ![]() 或x=3(舍),
或x=3(舍),
②当2S△PDB=S△CDB时,
∴2PD=CD,
即:|﹣x2+3x|=2|﹣x+3|,
∴x=±2或x=3(舍),
即:综上所述,x=± ![]() 或x=±2
或x=±2
(4)![]()
【解析】解:(4)直线AB解析式为y=﹣x+3,
∴线段AB的垂直平分线l的解析式为y=x,
∵过点B,C,P的外接圆恰好经过点A,
∴过点B,C,P的外接圆的圆心既是线段AB的垂直平分线上,也在线段PC的垂直平分线上,
∴ ![]() ,
,
∴x=± ![]() ,
,
所以答案是: ![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目