题目内容
【题目】如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从点B出发,沿BC以2cm/s的速度向点C移动,点Q从点C出发,以1cm/s的速度向点A移动,若点P、Q分别从点B、C同时出发,设运动时间为t s,当t=时,△CPQ与△CBA相似.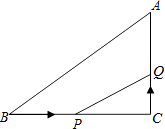
【答案】4.8或 ![]()
【解析】解:CP和CB是对应边时,△CPQ∽△CBA,
所以, ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得t=4.8;
CP和CA是对应边时,△CPQ∽△CAB,
所以, ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得t= ![]() .
.
综上所述,当t=4.8或 ![]() 时,△CPQ与△CBA相似.
时,△CPQ与△CBA相似.
所以答案是4.8或 ![]() .
.
【考点精析】利用勾股定理的概念和相似三角形的判定对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目