Question

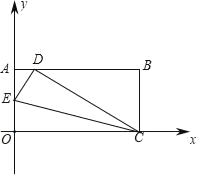
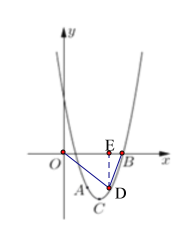
【题目】如图，在平面直角坐标系中，抛物线经过点和点，顶点为.

（1）求这条抛物线的表达式和顶点的坐标；

（2）点关于抛物线对称轴的对应点为点，联结，求的正切值；

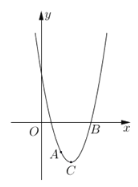
（3）将抛物线向上平移个单位，使顶点落在点处，点落在点处，如果，求的值.

Answer 1

【答案】（1），；（2）3；（3）

【解析】

(1)根据待定系数法，即可求解；

(2)根据题意，画出图形，由OD=，OB=5，可得：∠OBD=∠ODB，即可求解；

(3)根据题意：可得：BE=，BF=t，列出关于t的方程，即可求解.

（1）∵抛物线经过点和点，

∴，解得：，

∴抛物线的表达式是：，

即：，

∴；

（2）∵抛物线的对称轴是：直线x=3，点关于抛物线对称轴的对应点为点，

∴点D的坐标（4，-3），

∴OD=，

∵OB=5，

∴OB=OD，

∴∠OBD=∠ODB，

过点D作DE⊥x轴，则DE=3，BE=5-4=1，

∴tan∠ODB=tan∠OBD==3；

（3）∵抛物线向上平移个单位，使顶点落在点处，点落在点处，

∴E（3，-4+t），F（5，t），

∴BE==，BF=t，

∵，

∴=t，解得：t=.