Question

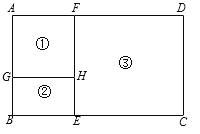
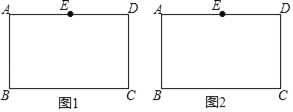
【题目】如图，在矩形ABCD中，点E为AD的中点，不用圆规、量角器等工具，只用无刻度的直尺作图．

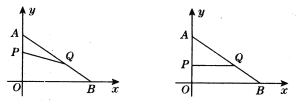
（1）如图1，在BC上找点F，使点F是BC的中点；

（2）如图2，连接AC，在AC上取两点P，Q，使P，Q是AC的三等分点．

Answer 1

【答案】（1）详见解析；（2）详见解析.

【解析】

（1）根据矩形的对角线相等且互相平分作出图形即可；

（2）根据矩形的性质和三角形中位线定理作出图形即可．

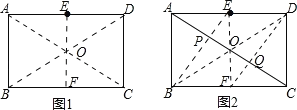
（1）如图1，连接AC、BD交于点O，延长EO交BC于F，则点F即为所求．

证明如下：

∵ABCD是矩形，

∴BO=OD，AD∥BC，AD=BC，

∴∠EDO=∠FBO．

∵∠EOD=∠FOB，

∴△EOD≌△FOB，

∴ED=FB=AD=BC，

∴F为BC的中点．

（2）如图2，BD交AC于O，延长EO交BC于F．

连接EB交AC于P，连接DF交AC于Q，则P、Q即为所求．

证明如下：

由（1）可得：F为BC的中点，

∴ED=BF=AE=FC，ED∥BF，

∴四边形EBFD是平行四边形，

∴BE∥FD．

∵FC=BF，

∴CQ=PQ．

∵AD∥BC，

∴∠EAC=∠FCA，∠ADQ=∠CFQ．

∵BE∥FD，

∴∠AEP=∠ADQ，

∴∠AEP=∠CFQ．

在△AEP和△CFQ中，

∵∠EAC=∠FCA，AE=CF，∠AEP=∠CFQ，

∴△AEP≌△CFQ，

∴AP=CQ，

∴AP=PQ=CQ，

∴P，Q是AC的三等分点．