Question

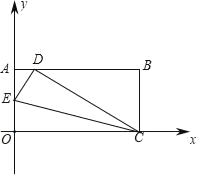
【题目】将一矩形纸片OABC放在直角坐标系中，O为原点C在x轴上，OA＝5，OC＝13，如图所示，在OA上取一点E，将△EOC沿EC折叠，使O点落在AB边上的D点，则E点坐标为_____．

Answer 1

【答案】（0，）．

【解析】

先根据折叠的性质得出DC=OC=13，在Rt△BCD中，运用矩形的性质及勾股定理得出BD=12，然后在Rt△AED中，由勾股定理得OE2=12+（5-OE）2，解方程求出OE的长，进而求出点E的坐标．

解：∵四边形OABC是矩形，

∴BC＝OA＝5，AB＝OC＝13，∠OAB＝∠B＝90°，

∵将△EOC沿EC折叠，使O点落在AB边上的D点，

∴DC＝OC＝13，DE＝OE，

在Rt△BCD中，∵∠B＝90°，BC＝5，CD＝13，

∴BD＝＝＝12．

∴AD＝AB﹣BD＝1，

在Rt△AED中，AD＝1，DE＝OE，AE＝5﹣OE，

∴DE2＝AD2+AE2，即OE2＝12+（5﹣OE）2，

解得：OE＝，

∴E点的坐标为（0，）；

故答案为：（0，）．